Difference between revisions of "Airy Bi"
(→Properties) |
|||
| Line 17: | Line 17: | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<strong>Proof:</strong> Suppose that $y$ has the form | <strong>Proof:</strong> Suppose that $y$ has the form | ||
| − | $$y(z) = \displaystyle\int_{C} f(t)e^{zt} dt,$$ | + | $$y(z) = \displaystyle\int_{C} f(t)e^{-zt} dt,$$ |
where $C$ is an as-of-yet undefined contour in the complex plane. Assuming that we may differentiate under the integral it is clear that | where $C$ is an as-of-yet undefined contour in the complex plane. Assuming that we may differentiate under the integral it is clear that | ||
| − | $$y''(z)=\displaystyle\int_{C} f(t)t^2 e^{zt} dt.$$ | + | $$y''(z)=\displaystyle\int_{C} f(t)t^2 e^{-zt} dt.$$ |
Thus we plug this representation into the differential equation to get | Thus we plug this representation into the differential equation to get | ||
| − | $$(*) \hspace{35pt} y''(z)-zy(z) = \displaystyle\int_{C} (t^2-z)f(t)e^{zt} dt = 0.$$ | + | $$(*) \hspace{35pt} y''(z)-zy(z) = \displaystyle\int_{C} (t^2-z)f(t)e^{-zt} dt = 0.$$ |
Now we integrate by parts to see | Now we integrate by parts to see | ||
$$\begin{array}{ll} | $$\begin{array}{ll} | ||
| − | \displaystyle\int_{C} zf(t)e^{zt} dt &= \displaystyle\int_{C} f(t) \dfrac{d}{dt} e^{zt} dt \\ | + | \displaystyle\int_{C} zf(t)e^{-zt} dt &= -\displaystyle\int_{C} f(t) \dfrac{d}{dt} e^{-zt} dt \\ |
| − | &= -f(t)e^{zt} \Bigg |_{C} + \displaystyle\int_{C} f'(t)e^{zt} dt. | + | &= -f(t)e^{zt} \Bigg |_{C} + \displaystyle\int_{C} f'(t)e^{-zt} dt. |
\end{array}$$ | \end{array}$$ | ||
We will pick the contour $C$ to enforce $f(t)e^{zt} \Bigg |_{C}=0$. We will do this by first determining the function $f$. Plugging this back into the formula $(*)$ yields | We will pick the contour $C$ to enforce $f(t)e^{zt} \Bigg |_{C}=0$. We will do this by first determining the function $f$. Plugging this back into the formula $(*)$ yields | ||
| Line 34: | Line 34: | ||
We have the freedom to choose $f$ and $C$. We will choose $f$ so that | We have the freedom to choose $f$ and $C$. We will choose $f$ so that | ||
$$t^2f(t)-f'(t)=0.$$ | $$t^2f(t)-f'(t)=0.$$ | ||
| − | This is a simple differential equation | + | This is a simple differential equation with [http://www.wolframalpha.com/input/?i=t^2f%28t%29-f%27%28t%29%3D0 a solution] |
| − | $$f(t)= | + | $$f(t)=e^{\frac{t^3}{3}}.$$ |
So we have derived | So we have derived | ||
| − | $$y(z)=\displaystyle\int_{C} e^{zt + \frac{t^3}{3}} dt.$$ | + | $$y(z)=\displaystyle\int_{C} e^{-zt + \frac{t^3}{3}} dt.$$ |
To pick the contour $C$ note that the integrand of $y$ is an [[entire function]] and hence if $C$ is a simple closed curve we would have $y(z)=0$ for all $z \in \mathbb{C}$. | To pick the contour $C$ note that the integrand of $y$ is an [[entire function]] and hence if $C$ is a simple closed curve we would have $y(z)=0$ for all $z \in \mathbb{C}$. | ||
The variable of the integral defining $y$ is $t$ and for $t \in \mathbb{C}$ with $|t|$ very large, the cubic term in the exponent dominates. Hence consider polar form $t=|t|e^{i\theta}$ and compute | The variable of the integral defining $y$ is $t$ and for $t \in \mathbb{C}$ with $|t|$ very large, the cubic term in the exponent dominates. Hence consider polar form $t=|t|e^{i\theta}$ and compute | ||
$$e^{\frac{t^3}{3}} = \exp\left( \frac{|t|^3 e^{3i\theta}}{3} \right).$$ | $$e^{\frac{t^3}{3}} = \exp\left( \frac{|t|^3 e^{3i\theta}}{3} \right).$$ | ||
| − | Notice that the inequality $\mathrm{Re} \hspace{2pt} e^{3i\theta} \leq 0$ forces $\cos(3\theta)\leq 0$ yielding three sectors defined by $\theta$: [[File:Airysectors.png|200px]] | + | Notice that the inequality $\mathrm{Re} \hspace{2pt} e^{3i\theta} \leq 0$ forces $\cos(3\theta)\leq 0$ [http://www.wolframalpha.com/input/?i=cos%283*theta%29%3C0 yielding] three sectors defined by $\theta$: [[File:Airysectors.png|200px]] |
$$-\dfrac{\pi}{2} \leq \theta \leq -\dfrac{\pi}{6},$$ | $$-\dfrac{\pi}{2} \leq \theta \leq -\dfrac{\pi}{6},$$ | ||
$$\dfrac{\pi}{6} \leq \theta \leq \dfrac{\pi}{2},$$ | $$\dfrac{\pi}{6} \leq \theta \leq \dfrac{\pi}{2},$$ | ||
$$\dfrac{9\pi}{6} \leq \theta \leq \dfrac{11\pi}{6}.$$ | $$\dfrac{9\pi}{6} \leq \theta \leq \dfrac{11\pi}{6}.$$ | ||
| − | Notice that the first two of these sectors includes the entire $y$-axis in the complex plane. Hence we will take our contour $C$ to be the $y$ axis directed from $-i\infty$ toward $+i\infty$. This yields finally | + | We will consider three contours $C_1,C_2,C_3$, where each contour $C_i$ has endpoints at complex $\infty$ in different sectors. Call the left sector $\gamma$, the upper-right sector $\beta$ and the lower-right sector $\alpha$. Let $C_1$ be oriented from sector $\alpha$ to sector $\beta$ (this sort of curve is labelled as "$C$" in the image above), $C_2$ from sector $\beta$ to sector $\gamma$, and $C_3$ from sector $\gamma$ to sector $\alpha$. By our analysis we have derived three solutions to Airy's equation: |
| + | $$y_i(z) = \displaystyle\int_{C_i} e^{-zt + \frac{t^3}{3}} dt;i=1,2,3$$ | ||
| + | Since these functions satisfy a second order differential equation, it is impossible for them to be [[linearly independent]]. Now notice that we can compute | ||
| + | $$\displaystyle\int_{C_1\cup C_2 \cup C_3} e^{-zt + \frac{t^3}{3}} dt = 0.$$ | ||
| + | Therefore | ||
| + | $$y_1(z)+y_2(z)+y_3(z)=0.$$ | ||
| + | |||
| + | Notice that the first two of these sectors includes the entire $y$-axis in the complex plane.0 Hence we will take our contour $C$ to be the $y$ axis directed from $-i\infty$ toward $+i\infty$. This yields finally | ||
$$y(z)=\displaystyle\int_{-i\infty}^{i\infty} e^{zt+\frac{t^3}{3}} dt.$$ | $$y(z)=\displaystyle\int_{-i\infty}^{i\infty} e^{zt+\frac{t^3}{3}} dt.$$ | ||
</div> | </div> | ||
Revision as of 03:53, 16 January 2015
The Airy function $\mathrm{Ai}$ in the complex plane are given by $$\mathrm{Ai}(z) = \dfrac{1}{2\pi i} \displaystyle\int_{-i\infty}^{i\infty}\exp \left( \dfrac{t^3}{3} - zt \right) dt$$ and $$\mathrm{Bi}(x) = \dfrac{1}{\pi} \displaystyle\int_0^{\infty} \left[ e^{-\frac{t^3}{3} + xt} + \sin \left( \dfrac{t^3}{3}+xt \right) \right] dt.$$
- Airyai.png
Airy $\mathrm{Ai}$ function.
- Airybi.png
Bairy $\mathrm{Bi}$ function.
Properties
Theorem: The function $\mathrm{Ai}$ is a solution to the differential equation $$y(z) - zy(z) = 0.$$
Proof: Suppose that $y$ has the form $$y(z) = \displaystyle\int_{C} f(t)e^{-zt} dt,$$ where $C$ is an as-of-yet undefined contour in the complex plane. Assuming that we may differentiate under the integral it is clear that $$y(z)=\displaystyle\int_{C} f(t)t^2 e^{-zt} dt.$$ Thus we plug this representation into the differential equation to get $$(*) \hspace{35pt} y(z)-zy(z) = \displaystyle\int_{C} (t^2-z)f(t)e^{-zt} dt = 0.$$ Now we integrate by parts to see $$\begin{array}{ll} \displaystyle\int_{C} zf(t)e^{-zt} dt &= -\displaystyle\int_{C} f(t) \dfrac{d}{dt} e^{-zt} dt \\ &= -f(t)e^{zt} \Bigg |_{C} + \displaystyle\int_{C} f'(t)e^{-zt} dt. \end{array}$$ We will pick the contour $C$ to enforce $f(t)e^{zt} \Bigg |_{C}=0$. We will do this by first determining the function $f$. Plugging this back into the formula $(*)$ yields $$\begin{array}{ll} 0 &= y(z) - zy(z) \\ &= f(t)e^{zt} \Bigg |_{C} + \displaystyle\int_{C} (t^2f(t)-f'(t))e^{zt} dt. \end{array}$$ We have the freedom to choose $f$ and $C$. We will choose $f$ so that $$t^2f(t)-f'(t)=0.$$ This is a simple differential equation with a solution $$f(t)=e^{\frac{t^3}{3}}.$$ So we have derived $$y(z)=\displaystyle\int_{C} e^{-zt + \frac{t^3}{3}} dt.$$ To pick the contour $C$ note that the integrand of $y$ is an entire function and hence if $C$ is a simple closed curve we would have $y(z)=0$ for all $z \in \mathbb{C}$.
The variable of the integral defining $y$ is $t$ and for $t \in \mathbb{C}$ with $|t|$ very large, the cubic term in the exponent dominates. Hence consider polar form $t=|t|e^{i\theta}$ and compute
$$e^{\frac{t^3}{3}} = \exp\left( \frac{|t|^3 e^{3i\theta}}{3} \right).$$
Notice that the inequality $\mathrm{Re} \hspace{2pt} e^{3i\theta} \leq 0$ forces $\cos(3\theta)\leq 0$ yielding three sectors defined by $\theta$: 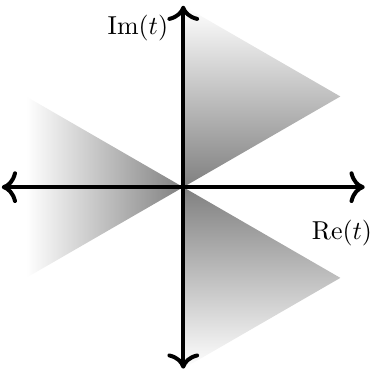 $$-\dfrac{\pi}{2} \leq \theta \leq -\dfrac{\pi}{6},$$
$$\dfrac{\pi}{6} \leq \theta \leq \dfrac{\pi}{2},$$
$$\dfrac{9\pi}{6} \leq \theta \leq \dfrac{11\pi}{6}.$$
$$-\dfrac{\pi}{2} \leq \theta \leq -\dfrac{\pi}{6},$$
$$\dfrac{\pi}{6} \leq \theta \leq \dfrac{\pi}{2},$$
$$\dfrac{9\pi}{6} \leq \theta \leq \dfrac{11\pi}{6}.$$
We will consider three contours $C_1,C_2,C_3$, where each contour $C_i$ has endpoints at complex $\infty$ in different sectors. Call the left sector $\gamma$, the upper-right sector $\beta$ and the lower-right sector $\alpha$. Let $C_1$ be oriented from sector $\alpha$ to sector $\beta$ (this sort of curve is labelled as "$C$" in the image above), $C_2$ from sector $\beta$ to sector $\gamma$, and $C_3$ from sector $\gamma$ to sector $\alpha$. By our analysis we have derived three solutions to Airy's equation: $$y_i(z) = \displaystyle\int_{C_i} e^{-zt + \frac{t^3}{3}} dt;i=1,2,3$$ Since these functions satisfy a second order differential equation, it is impossible for them to be linearly independent. Now notice that we can compute $$\displaystyle\int_{C_1\cup C_2 \cup C_3} e^{-zt + \frac{t^3}{3}} dt = 0.$$ Therefore $$y_1(z)+y_2(z)+y_3(z)=0.$$
Notice that the first two of these sectors includes the entire $y$-axis in the complex plane.0 Hence we will take our contour $C$ to be the $y$ axis directed from $-i\infty$ toward $+i\infty$. This yields finally $$y(z)=\displaystyle\int_{-i\infty}^{i\infty} e^{zt+\frac{t^3}{3}} dt.$$