Difference between revisions of "Arcsinh"
(→Properties) |
|||
| Line 10: | Line 10: | ||
=Properties= | =Properties= | ||
| − | + | {{:Derivative of arcsinh}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=References= | =References= | ||
Revision as of 19:15, 15 May 2016
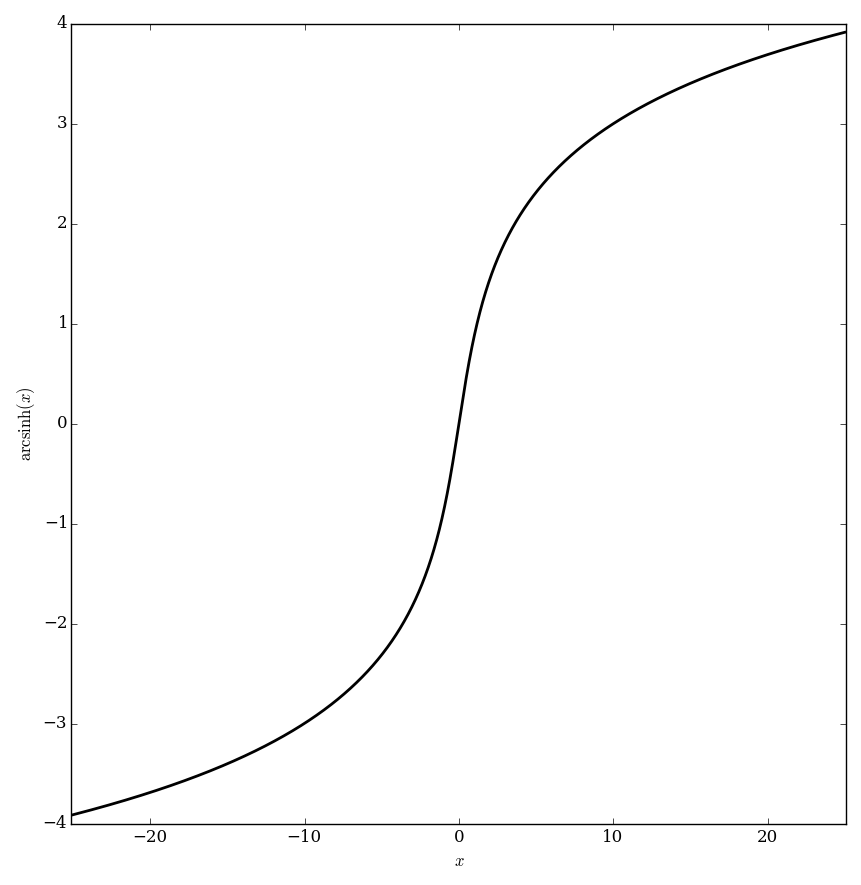
The $\mathrm{arcsinh}$ function is the inverse function of the hyperbolic sine function defined by $$\mathrm{arcsinh}(z)=\log\left(z+\sqrt{1+z^2}\right).$$
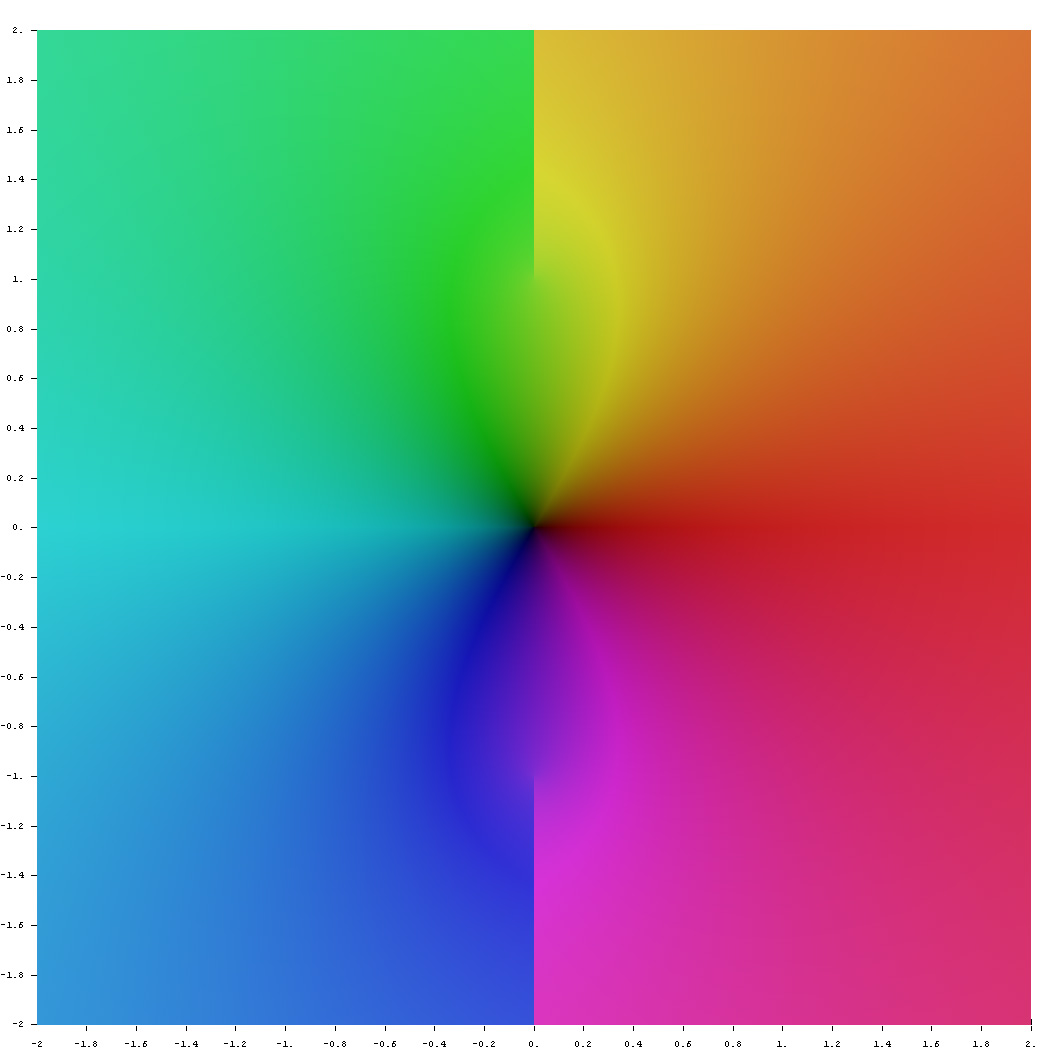
Domain coloring of analytic continuation of $\mathrm{arcsinh}$.
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arcsinh}(z) = \dfrac{1}{\sqrt{1+z^2}},$$ where $\mathrm{arcsinh}$ denotes the inverse hyperbolic sine.
Proof
From the definition, $$\mathrm{arcsinh}(z)=\log \left(z + \sqrt{1+z^2} \right).$$ Using derivative of logarithm and the chain rule, $$\begin{array}{ll} \dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arcsinh}(z) &= \dfrac{\mathrm{d}}{\mathrm{d}z} \log \left(z + \sqrt{1+z^2} \right) \\ &= \dfrac{1}{z+\sqrt{1+z^2}} \dfrac{\mathrm{d}}{\mathrm{d}z} \Bigg[ z + \sqrt{1+z^2} \Bigg] \\ &= \dfrac{1+\frac{z}{\sqrt{1+z^2}}}{z+\sqrt{1+z^2}} \\ &= \dfrac{\sqrt{1+z^2}+z}{z\sqrt{1+z^2}+1+z^2} \\ &= \dfrac{\sqrt{1+z^2}+z}{z\sqrt{1+z^2}+1+z^2} \left( \dfrac{\sqrt{1+z^2}-z}{\sqrt{1+z^2}-z} \right) \\ &= \dfrac{1}{z(1+z^2)+\sqrt{1+z^2}+z^2\sqrt{1+z^2}-z^2\sqrt{1+z^2}-z-z^3} \\ &= \dfrac{1}{\sqrt{1+z^2}}, \end{array}$$ as was to be shown.