Difference between revisions of "Barnes G"
From specialfunctionswiki
| (7 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
<gallery> | <gallery> | ||
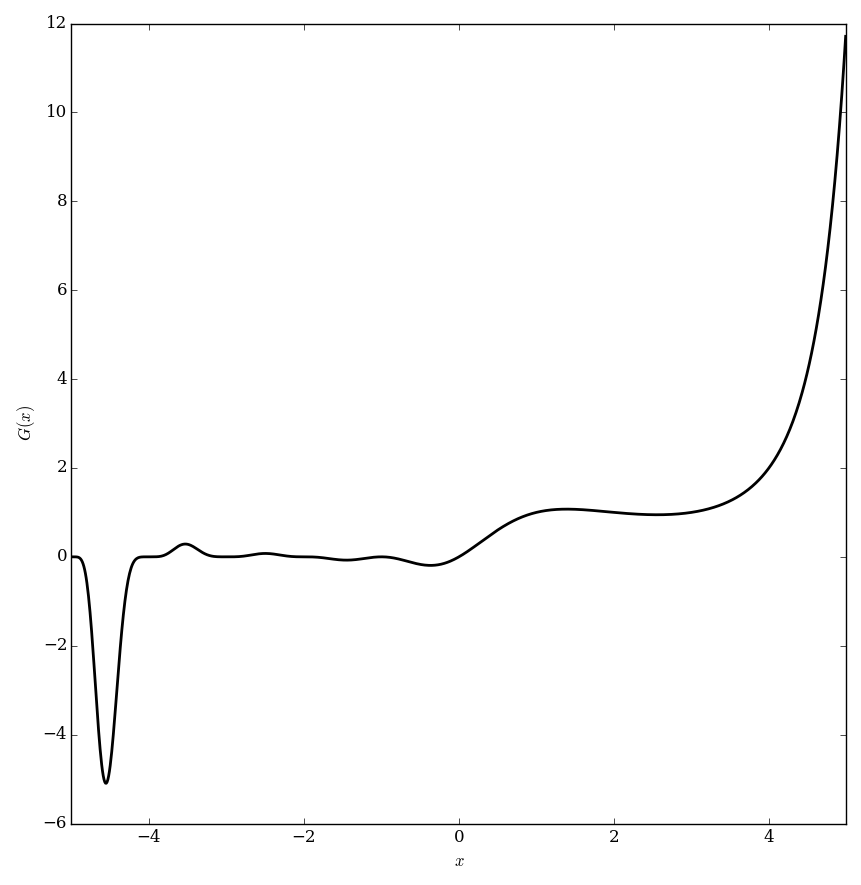
File:Barnesgplot.png|Graph of $G$. | File:Barnesgplot.png|Graph of $G$. | ||
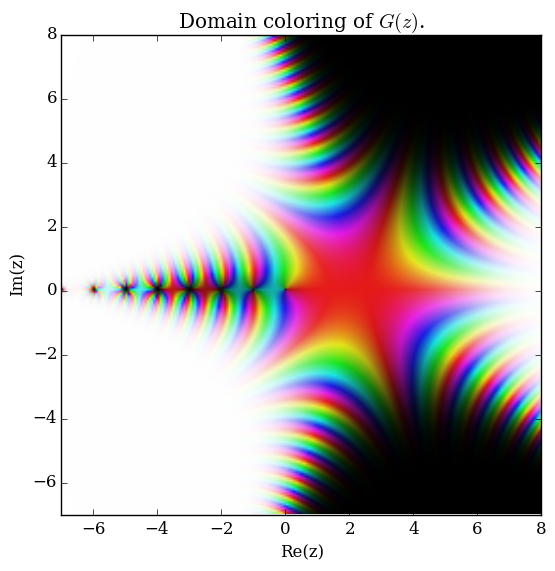
| + | File:Complexbarnesgplot.png|[[Domain coloring]] of $G$. | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
=Properties= | =Properties= | ||
| − | < | + | [[Barnes G at z+1 in terms of Barnes G and gamma]]<br /> |
| − | < | + | [[Barnes G at positive integer]]<br /> |
| − | + | ||
| − | + | =References= | |
| − | + | [http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0031%7CLOG_0022 The theory of the $G$-function by E.W. Barnes] | |
| − | |||
| − | |||
| − | |||
| − | + | [[Category:SpecialFunction]] | |
| − | + | [[Category:Definition]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 05:48, 6 June 2016
The Barnes $G$ function is defined by the following Weierstrass factorization: $$G(1+z)=(2\pi)^{\frac{z}{2}} \exp \left( - \dfrac{z+z^2(1+\gamma)}{2} \right) \displaystyle\prod_{k=1}^{\infty} \left\{ \left( 1+\dfrac{z}{k} \right)^k \exp \left( \dfrac{z^2}{2k}-z \right) \right\},$$ where $\exp$ denotes the exponential function and $\gamma$ denotes the Euler-Mascheroni constant.
Domain coloring of $G$.
Properties
Barnes G at z+1 in terms of Barnes G and gamma
Barnes G at positive integer