Difference between revisions of "Coth"
m (Tom moved page Hyperbolic cotangent to Coth) |
|||
| Line 1: | Line 1: | ||
| − | [[File:Complex_Coth.jpg| | + | The hyperbolic cotangent is defined by |
| + | $$\mathrm{coth}(z)=\dfrac{1}{\tanh(z)},$$ | ||
| + | where $\tanh$ denotes the [[Tanh|hyperbolic tangent]] function. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
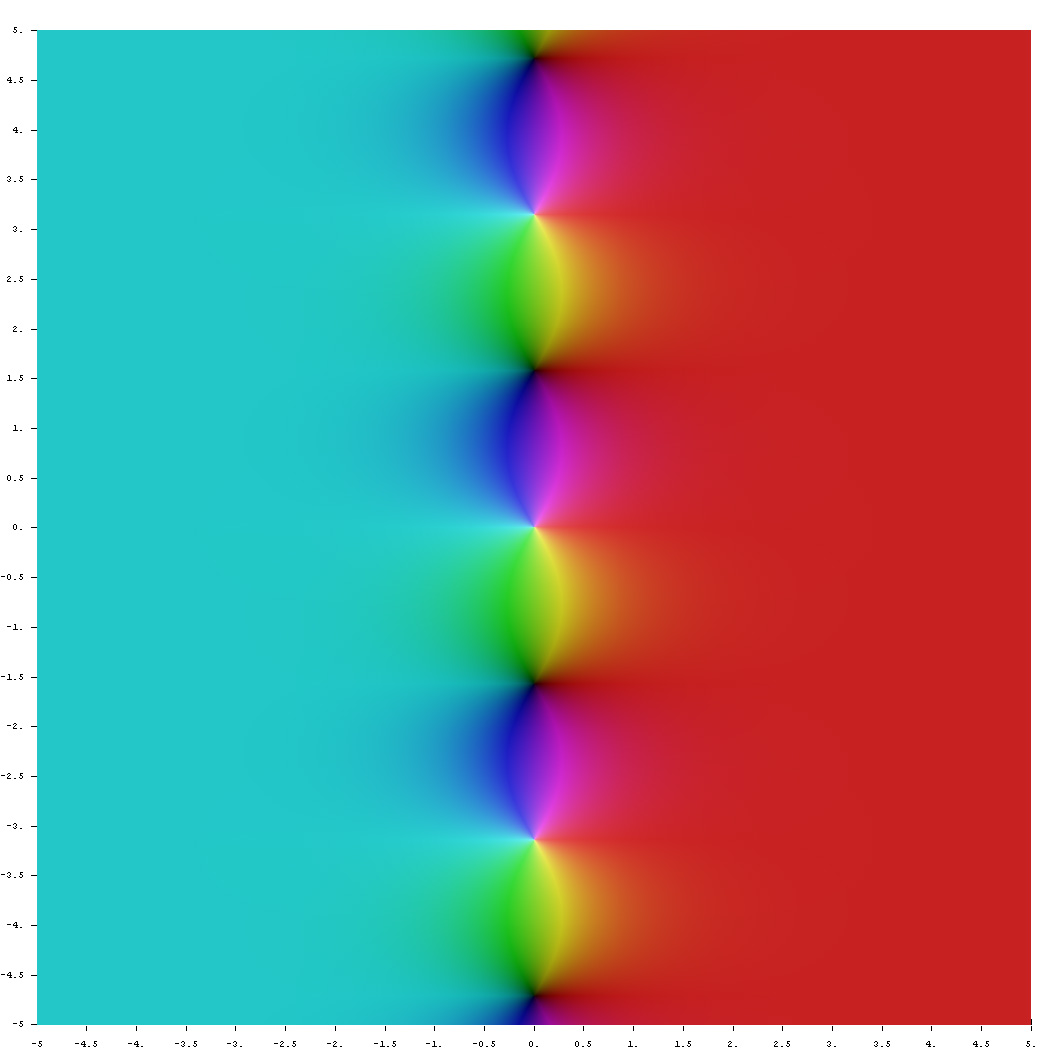
| + | File:Complex_Coth.jpg|[[Domain coloring]] of [[analytic continuation of $\mathrm{coth}$]]. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | {{:Derivative of coth}} | ||
| + | |||
| + | <center>{{:Hyperbolic trigonometric functions footer}}</center> | ||
Revision as of 05:48, 20 March 2015
The hyperbolic cotangent is defined by $$\mathrm{coth}(z)=\dfrac{1}{\tanh(z)},$$ where $\tanh$ denotes the hyperbolic tangent function.
Domain coloring of [[analytic continuation of $\mathrm{coth}$]].
Contents
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{coth}(z) = -\mathrm{csch}^2(z),$$ where $\mathrm{coth}$ denotes the hyperbolic cotangent and $\mathrm{csch}$ denotes the hyperbolic cosecant.
Proof
By the definition, $$\mathrm{coth}(z) = \dfrac{\mathrm{cosh}(z)}{\mathrm{sinh}(z)}.$$ Using the quotient rule, the derivative of sinh, the derivative of cosh, Pythagorean identity for sinh and cosh, and the definition of $\mathrm{csch}$, we see $$\begin{array}{ll} \dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{coth}(z) &= \dfrac{\sinh^2(z)-\cosh^2(z)}{\mathrm{sinh}^2(z)} \\ &= - \dfrac{\mathrm{cosh}^2(z)-\mathrm{sinh}^2(z)}{\mathrm{sinh}^2(z)} \\ &= -\mathrm{csch}^2(z), \end{array}$$ as was to be shown.