Difference between revisions of "Derivative of arctan"
From specialfunctionswiki
| Line 1: | Line 1: | ||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
| − | <strong> | + | <strong>[[Derivative of arctan|Theorem]]:</strong> The following formula holds: |
$$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arctan}(z) = \dfrac{1}{z^2+1},$$ | $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arctan}(z) = \dfrac{1}{z^2+1},$$ | ||
where $\mathrm{arctan}$ denotes the [[arctan|inverse tangent]] function. | where $\mathrm{arctan}$ denotes the [[arctan|inverse tangent]] function. | ||
Revision as of 04:16, 16 May 2016
Theorem: The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arctan}(z) = \dfrac{1}{z^2+1},$$ where $\mathrm{arctan}$ denotes the inverse tangent function.
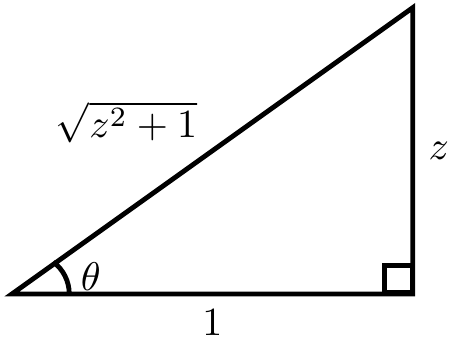
Proof: If $\theta=\mathrm{arctan}(z)$ then $\tan \theta = z$. Now use implicit differentiation with respect to $z$ yields $$\sec^2(\theta)\theta'=1.$$ The following triangle shows that $\sec^2(\mathrm{arctan}(z))=z^2+1$:
Substituting back in $\theta=\mathrm{arccos(z)}$ yields the formula $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arccos(z)} = \dfrac{1}{\sec^2(\mathrm{arctan(z)})} = \dfrac{1}{z^2+1},$$ as was to be shown. █