Difference between revisions of "Logarithm"
| Line 2: | Line 2: | ||
$$\log(x) = \displaystyle\int_1^x \dfrac{1}{t} dt.$$ | $$\log(x) = \displaystyle\int_1^x \dfrac{1}{t} dt.$$ | ||
The logarithm is the [[inverse function]] of [[exponential function|$e^x$]]. | The logarithm is the [[inverse function]] of [[exponential function|$e^x$]]. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
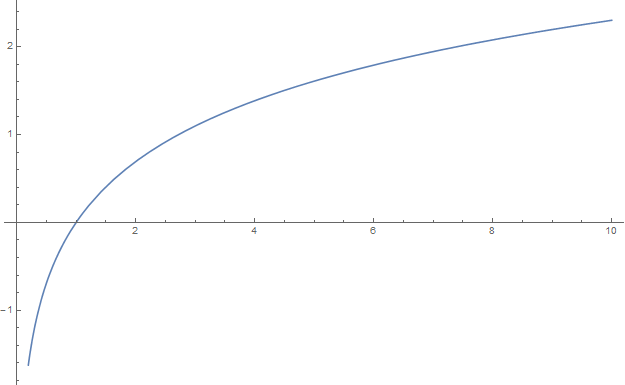
| + | File:Plotlogarithm.png|Graph of $\log$ on $(0,10]$. | ||
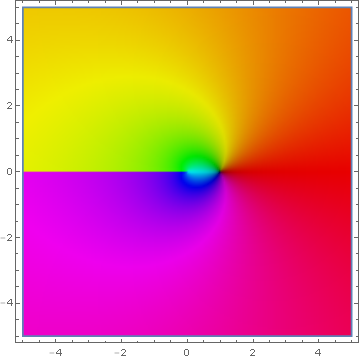
| + | File:Domcollogarithm.png|[[Domain coloring]] of [[analytic continuation]] of $\log$ with branch $(-\infty,0)$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
=Properties= | =Properties= | ||
Revision as of 14:27, 19 August 2015
For $x \in (0,\infty)$, the logarithm is defined by the formula $$\log(x) = \displaystyle\int_1^x \dfrac{1}{t} dt.$$ The logarithm is the inverse function of $e^x$.
Domain coloring of analytic continuation of $\log$ with branch $(-\infty,0)$.
Contents
Properties
Proposition: $\displaystyle\int \log(z) dz = z \log(z)-z$
Proof: █
Theorem: For $|z|<1$, $$\log(1+z) = -\displaystyle\sum_{k=1}^{\infty} \dfrac{(-1)^k z^k}{k}.$$
Proof: █
Relation to other special functions
Theorem
The following formula holds: $$\log(1+z)=z{}_2F_1(1,1;2;-z),$$ where $\log$ denotes the logarithm and ${}_2F_1$ denotes the hypergeometric pFq.
Proof
Calculate $$\begin{array}{ll} z{}_2F_1(1,1;2;-z) &= z\displaystyle\sum_{k=0}^{\infty} \dfrac{1^{\overline{k}}1^{\overline{k}}}{2^{\overline{k}}k!} (-z)^k \\ &= \displaystyle\sum_{k=0}^{\infty} \dfrac{\left( \frac{\Gamma(k+1)}{\Gamma(1)} \right)^2}{\left( \frac{\Gamma(2+k)}{\Gamma(2)} \right)k!}(-1)^k z^{k+1} \\ &= \displaystyle\sum_{k=0}^{\infty} \dfrac{(k!)^2(-1)^k}{(k+1)!k!} z^{k+1} \\ &= \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k}{k+1} z^{k+1} \\ &= -\displaystyle\sum_{k=1}^{\infty} \dfrac{(-1)^k z^k}{k} \\ &= \log(1+z), \end{array}$$ by the Taylor series of $\log(1+z)$. █
References
Theorem
The following formula holds for $x>0$: $$\mathrm{Ei}(x) = \gamma + \log x + \displaystyle\sum_{k=1}^{\infty} \dfrac{x^k}{kk!},$$ where $\mathrm{Ei}$ denotes the exponential integral Ei, $\log$ denotes the logarithm, and $\gamma$ denotes the Euler-Mascheroni constant.
Proof
References
- James Whitbread Lee Glaisher: On certain definite integrals involving the exponential-integral (1881)... (previous)... (next) (note: expresses the logarithm term as $\frac{1}{4}\log(x^4)$)
Theorem
The following formula holds: $$P(z)=\displaystyle\sum_{k=1}^{\infty} \dfrac{\mu(k)}{k} \log \zeta(kz),$$ where $P$ denotes the Prime zeta function, $\mu$ denotes the Möbius function, $\log$ denotes the logarithm, and $\zeta$ denotes the Riemann zeta function.