Difference between revisions of "Logarithmic integral"
From specialfunctionswiki
| Line 13: | Line 13: | ||
{{:Relationship between logarithmic integral and exponential integral}} | {{:Relationship between logarithmic integral and exponential integral}} | ||
{{:Prime number theorem, logarithmic integral}} | {{:Prime number theorem, logarithmic integral}} | ||
| + | |||
| + | =See Also= | ||
| + | [[Prime counting function]] <br /> | ||
Revision as of 21:13, 23 May 2016
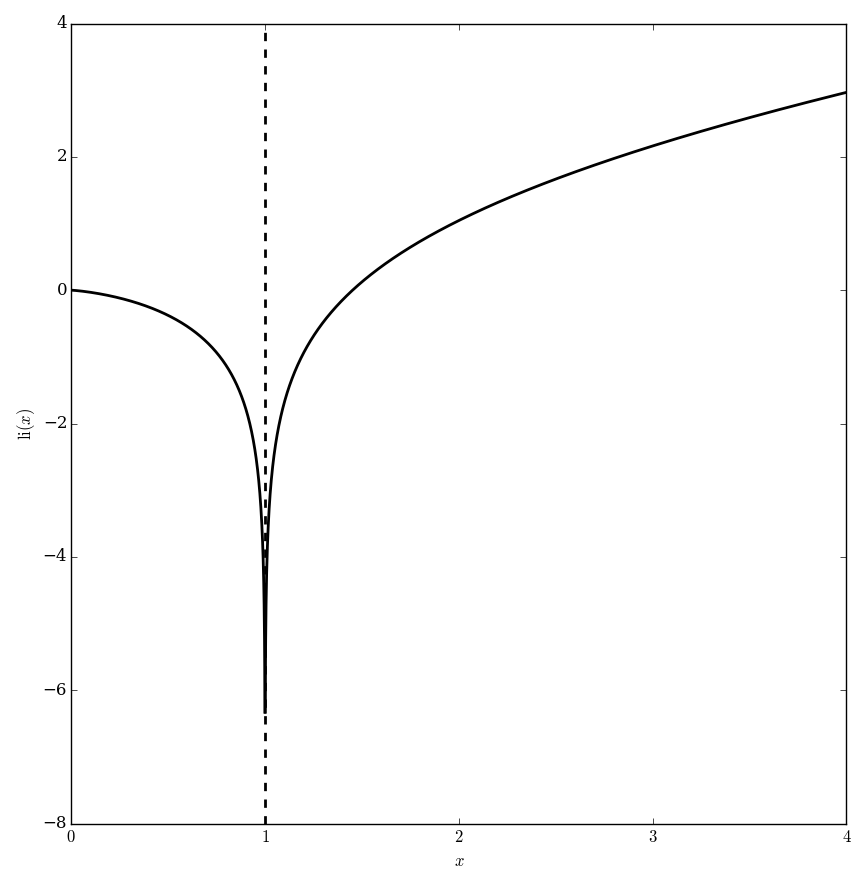
The logarithmic integral is $$\mathrm{li}(x) = \displaystyle\int_0^x \dfrac{dt}{\log(t)},$$ where $\log$ denotes the logarithm.
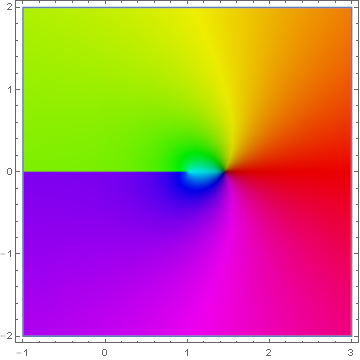
Domain coloring of analytic continuation of $\mathrm{li}$.
Contents
Properties
Theorem
The following formula holds: $$\mathrm{li}(x)=\mathrm{Ei}( \log(x)),$$ where $\mathrm{li}$ denotes the logarithmic integral, $\mathrm{Ei}$ denotes the exponential integral Ei, and $\log$ denotes the logarithm.
Proof
References
- James Whitbread Lee Glaisher: On certain definite integrals involving the exponential-integral (1881)... (previous)... (next) (note: expresses this relationship as $\mathrm{Ei}(x)=\mathrm{li}(e^x)$)
Theorem
The following formula holds: $$\lim_{x \rightarrow \infty} \dfrac{\pi(x)}{\mathrm{li}(x)}=1,$$ where $\pi$ denotes the prime counting function and $\mathrm{li}$ denotes the logarithmic integral.