Difference between revisions of "Riemann zeta"
From specialfunctionswiki
| Line 1: | Line 1: | ||
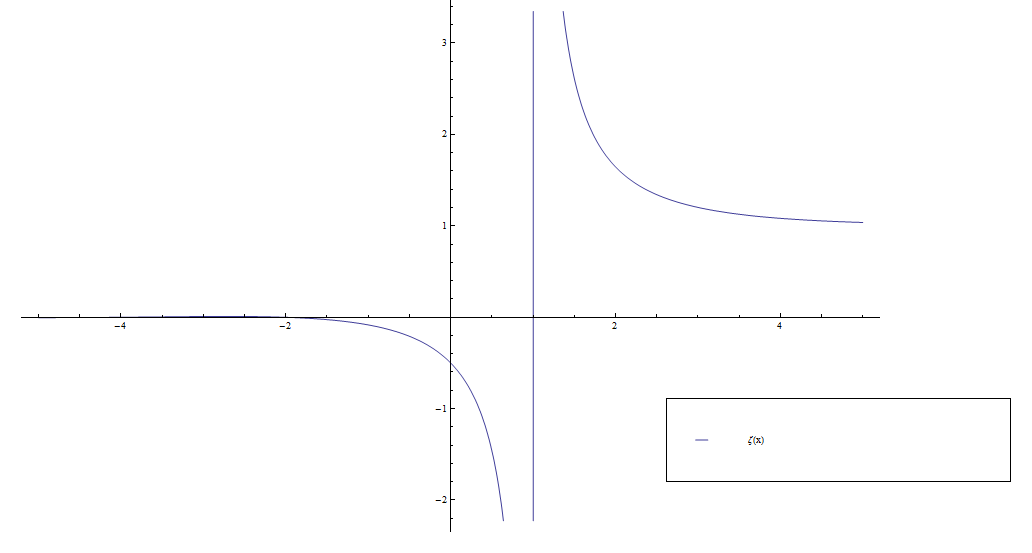
Consider the function $\zeta$ defined by the series | Consider the function $\zeta$ defined by the series | ||
| − | $$\zeta(z) = \displaystyle\sum_{ | + | $$\zeta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z}.$$ |
[[File:Riemannzeta.png|500px]] | [[File:Riemannzeta.png|500px]] | ||
Revision as of 06:17, 11 February 2015
Consider the function $\zeta$ defined by the series $$\zeta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z}.$$
Properties
Proposition: If $\mathrm{Re} \hspace{2pt} z > 1$, then the series defining $\zeta(z)$ converges.
Proof: █
Proposition (Euler Product): $\zeta(z)=\displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z} = \displaystyle\prod_{p \mathrm{\hspace{2pt} prime}} \dfrac{1}{1-p^{-z}}$
Proof: █
Proposition: Let $n$ be a positive integer. Then $$\zeta(2n)=(-1)^{n+1}\dfrac{B_{2n}(2\pi)^{2n}}{2(2n)!},$$ where $B_n$ denotes the Bernoulli numbers.
Proof: █