Difference between revisions of "Tangent"
| Line 22: | Line 22: | ||
<center>{{:Trigonometric functions footer}}</center> | <center>{{:Trigonometric functions footer}}</center> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Revision as of 18:44, 24 May 2016
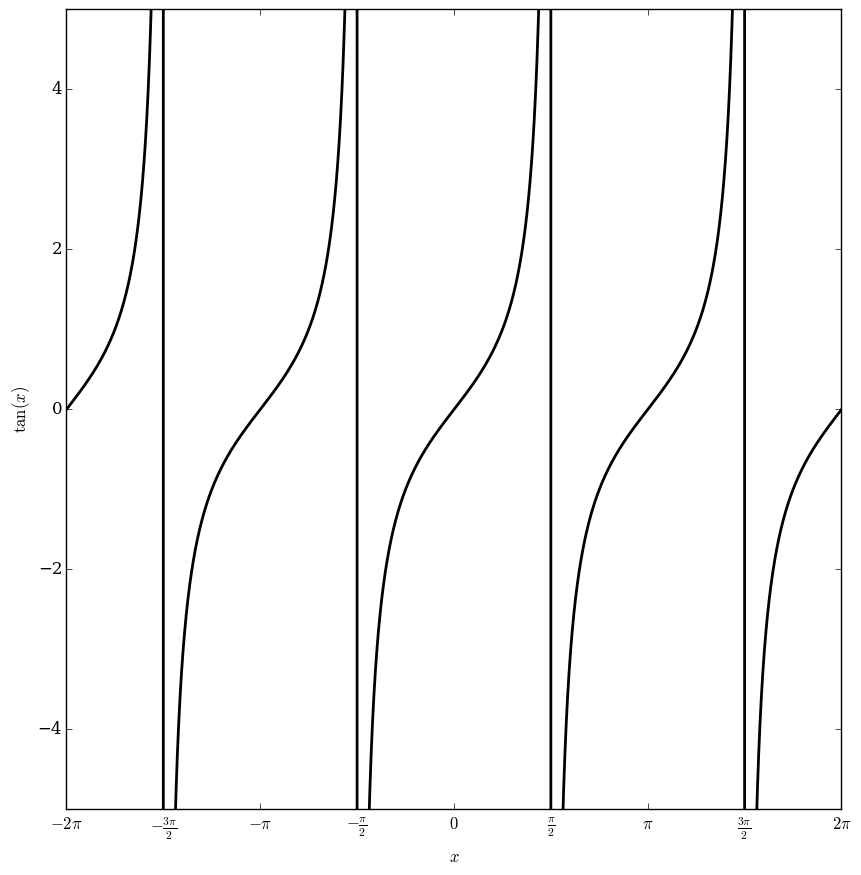
The tangent function is defined as the ratio of the sine and cosine functions: $$\tan(z) = \dfrac{\sin(z)}{\cos(z)}.$$
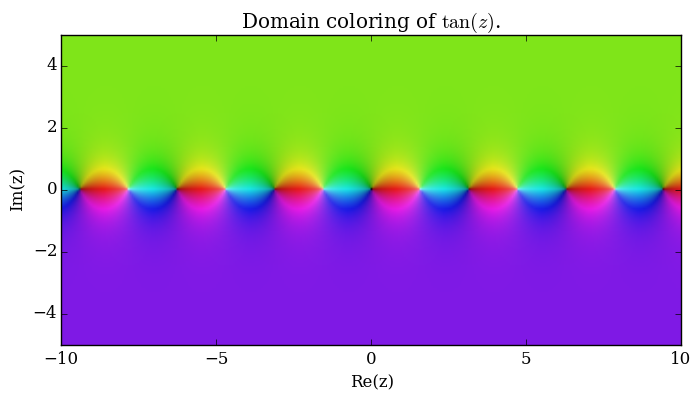
Domain coloring of $\tan$.
Contents
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \tan(z) = \sec^2(z),$$ where $\tan$ denotes the tangent function and $\sec$ denotes the secant function.
Proof
From the definition, $$\tan(z) = \dfrac{\sin(z)}{\cos(z)},$$ so using the quotient rule, the derivative of sine, the derivative of cosine, the Pythagorean identity for sin and cos, and the definition of secant, $$\dfrac{\mathrm{d}}{\mathrm{d}z} \tan(z) = \dfrac{\mathrm{d}}{\mathrm{d}z} \dfrac{\sin(z)}{\cos(z)} = \dfrac{\cos^2(z) + \sin^2(z)}{\cos^2(z)} = \dfrac{1}{\cos^2(z)} = \sec^2(z),$$ as was to be shown. $\blacksquare$
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.3.107$
Theorem
The following formula holds: $$\tan(z)=-i\tanh(iz),$$ where $\tan$ is the tangent and $\tanh$ is the hyperbolic tangent.
Proof
References
Theorem
The following formula holds: $$\tanh(z)=-i \tan(iz),$$ where $\tanh$ is the hyperbolic tangent and $\tan$ is the tangent.
Proof
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.5.9$
Theorem
The following formula holds: $$\tan(\mathrm{gd}(x))=\sinh(x),$$ where $\tan$ denotes tangent, $\mathrm{gd}$ denotes the Gudermannian, and $\sinh$ denotes the hyperbolic sine.
Proof
References
Theorem
The following formula holds: $$\sinh(\mathrm{gd}^{-1}(x))=\tan(x),$$ where $\sinh$ is the hyperbolic sine, $\mathrm{gd}^{-1}$ is the inverse Gudermannian, and $\tan$ is the tangent.