Hankel H (1)

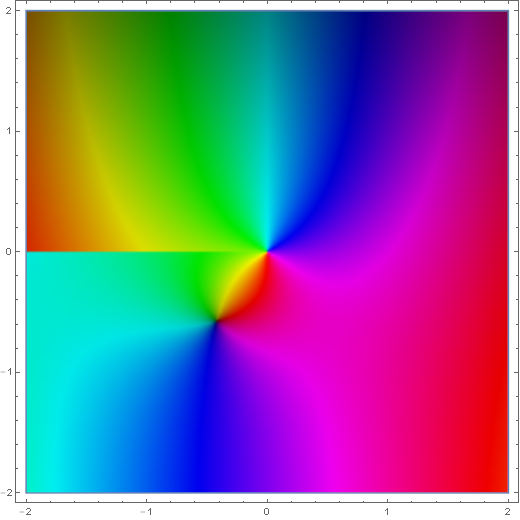
The Hankel functions of the first kind are defined by $$H_{\nu}^{(1)}(z)=J_{\nu}(z)+iY_{\nu}(z),$$ where $J_{\nu}$ is the Bessel function of the first kind and $Y_{\nu}$ is the Bessel function of the second kind. Note the similarity of these functions to the Hankel functions of the second kind.

• 

  Domain coloring of $H_1^{(1)}(z)$.

• 

  Bessel functions from Abramowitz&Stegun

See Also

Bessel $J$
Bessel $Y$

References

• 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 9.1.3

Hankel functions

Hankel $H_{\nu}^{(1)}$

Hankel $H_{\nu}^{(2)}$

Spherical Hankel $h_{\nu}^{(1)}$

Spherical Hankel $h_{\nu}^{(2)}$