Spherical Hankel h (1)

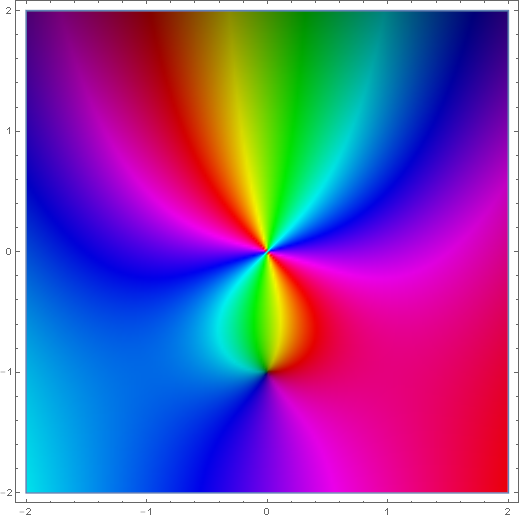
The spherical Hankel function $h_{\nu}^{(1)}$ is defined by $$h_{\nu}^{(1)}(z)=j_{\nu}(z)+iy_{\nu}(z),$$ where $j_{\nu}$ is the spherical Bessel function of the first kind and $y_{\nu}$ is the spherical Bessel function of the second kind.

• 

  Domain coloring of $h_1^{(1)}(z)$.

See Also

Spherical Bessel $j$
Spherical Bessel $y$

Hankel functions

Hankel $H_{\nu}^{(1)}$

Hankel $H_{\nu}^{(2)}$

Spherical Hankel $h_{\nu}^{(1)}$

Spherical Hankel $h_{\nu}^{(2)}$