Difference between revisions of "Gamma"
(→References) |
|||
| Line 145: | Line 145: | ||
=References= | =References= | ||
| + | [http://www.plouffe.fr/simon/math/Artin%20E.%20The%20Gamma%20Function%20%281931%29%2823s%29.pdf The Gamma Function by Emil Artin]<br /> | ||
| + | [http://ocw.mit.edu/courses/mathematics/18-104-seminar-in-analysis-applications-to-number-theory-fall-2006/projects/chan.pdf The sine product formula and the gamma function]<br /> | ||
[http://www.jstor.org/discover/10.2307/2309786?sid=21105065140641&uid=3739256&uid=2129&uid=70&uid=3739744&uid=4&uid=2 Leonhard Euler's Integral: A Historical Profile of the Gamma Function]<br /> | [http://www.jstor.org/discover/10.2307/2309786?sid=21105065140641&uid=3739256&uid=2129&uid=70&uid=3739744&uid=4&uid=2 Leonhard Euler's Integral: A Historical Profile of the Gamma Function]<br /> | ||
| − | |||
| − | |||
Revision as of 22:57, 13 January 2015
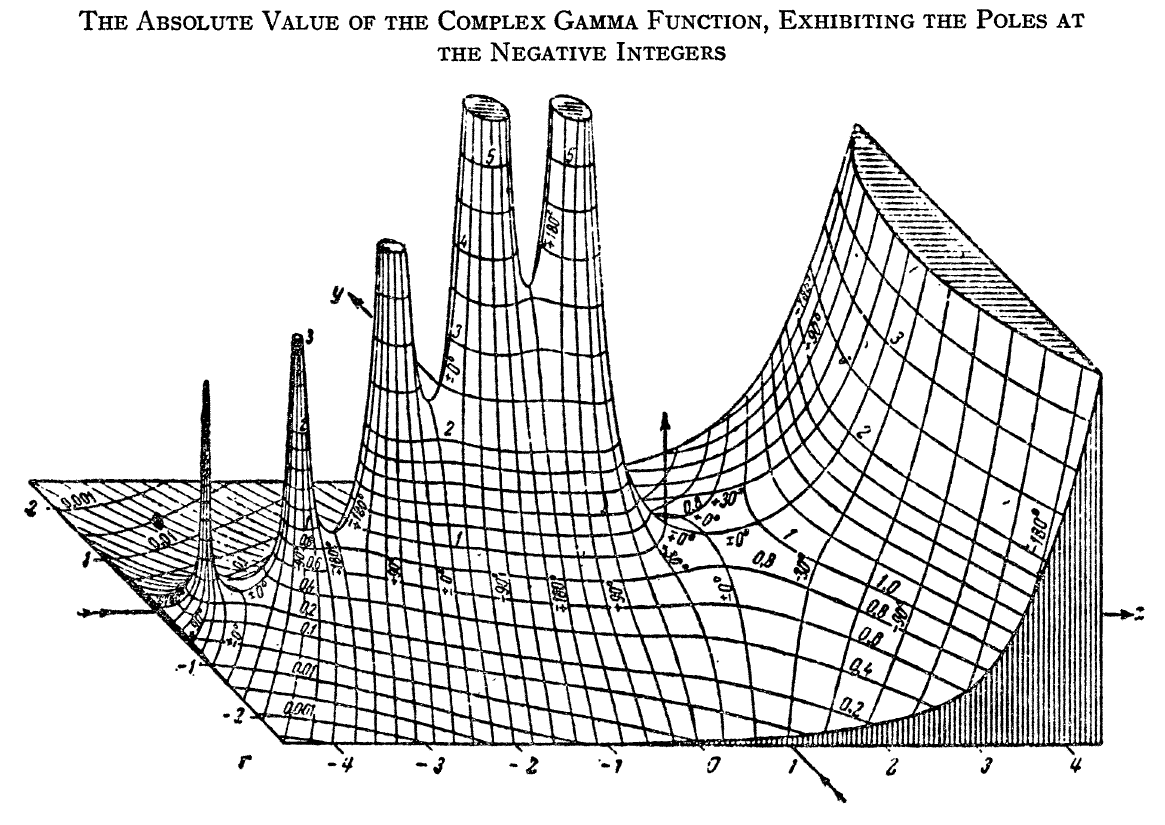
The gamma function is the function defined by the integral (initially for positive values of $x$) by the formula $$\Gamma(x)=\displaystyle\int_0^{\infty} \xi^{x-1}e^{-\xi} d\xi.$$ The analytic continuation of $\Gamma$ leads to a meromorphic function with poles at the negative integers.
- Gamma.png
Graph of $\Gamma$ on $[-7,7] \subset \mathbb{R}$.
- Complex gamma.jpg
Domain coloring of analytic continuation of $\Gamma$.
Contents
Recurrence
Proposition: $\Gamma(1)=1$
Proof: Compute directly $$\begin{array}{ll} \Gamma(1) &= \displaystyle\int_0^{\infty} \xi^{1-1} e^{-\xi} d\xi \\ &= \displaystyle\int_0^{\infty} e^{-\xi} d\xi \\ &= \left[ -e^{-\xi} \right]_{0}^{\infty} \\ &= 1.█ \end{array}$$
Theorem: $\Gamma(x+1)=x\Gamma(x); x>0$
Proof: Use integration by parts to compute $$\begin{array}{ll} \Gamma(x+1) &= \displaystyle\int_0^{\infty} \xi^x e^{-\xi} d\xi \\ &= -\xi^x e^{-\xi}|_0^{\infty} \displaystyle\int_0^{\infty} x \xi^{x-1} e^{-\xi} d\xi \\ &= x\Gamma(x).█ \end{array}$$
Corollary: If $x \in \mathbb{N}$, then $\Gamma(x+1)=x!$, where $x!$ denotes the factorial.
Other formulas
Proposition: The following formula holds $$\Gamma(x)=\lim_{k \rightarrow \infty} \dfrac{k!k^z}{z(z+1)\ldots(z+k)}.$$
Proof: █
Proposition: The following formula holds $$\dfrac{1}{\Gamma(z)} = ze^{\gamma z} \displaystyle\prod_{k=1}^{\infty} \left( 1 + \dfrac{z}{k}\right)e^{-\frac{z}{k}},$$ where $\gamma$ is the Euler-Mascheroni constant.
Proof: █
Proposition: The following formula holds $$\Gamma(x)=2\displaystyle\int_0^{\infty} e^{-t^2}t^{2x-1}dt.$$
Proof: █
Proposition: The following formula holds $$\displaystyle\int_0^{\frac{\pi}{2}} \cos^{2x-1}(\theta)\sin^{2y-1}(\theta) d\theta = \dfrac{\Gamma(x)\Gamma(y)}{2\Gamma(x+y)}.$$
Proof: █
$\Gamma(z)$ at half integers
Proposition: $\Gamma \left( \dfrac{1}{2} \right) = \sqrt{\pi}$.
Proof: █
Corollary: $\displaystyle\int_0^{\infty} e^{-t^2} dt = \dfrac{1}{2}\sqrt{\pi}$.
Other properties
Theorem (Convexity): The gamma function is logarithmically convex.
Proof: █
Theorem (Legendre Duplication Formula): $$\Gamma(2x)=\dfrac{2^{2x-1}}{\sqrt{\pi}} \Gamma(x)\Gamma \left( x +\dfrac{1}{2} \right).$$
Proof: █
Proposition: If $z=0,-1,-2,\ldots$ then $\Gamma(z)=\infty$.
Proof: proof goes here █
Theorem: The following relationship between $\Gamma$ and the $\sin$ function holds: $$\Gamma(x)\Gamma(1-x) = \dfrac{\pi}{\sin(\pi x)}.$$
Proof: proof goes here █
Proposition: $\Gamma(x) = \displaystyle\lim_{n \rightarrow \infty} \dfrac{n^x n!}{x(x+1)\ldots(x_n)}$
Proof: █
Proposition: $\Gamma(x)\Gamma(1-x)=\dfrac{\pi}{\sin(\pi x)}$
Proof: proof goes here █
Bohr-Mollerup Theorem: The gamma function is the unique function $f$ such that
- $f(1)=1$
- $f(x+1)=xf(x)$ for $x>0$
- $f$ is logarithmically convex.
Proof: █
References
The Gamma Function by Emil Artin
The sine product formula and the gamma function
Leonhard Euler's Integral: A Historical Profile of the Gamma Function