Difference between revisions of "Lambert W"
From specialfunctionswiki
| Line 1: | Line 1: | ||
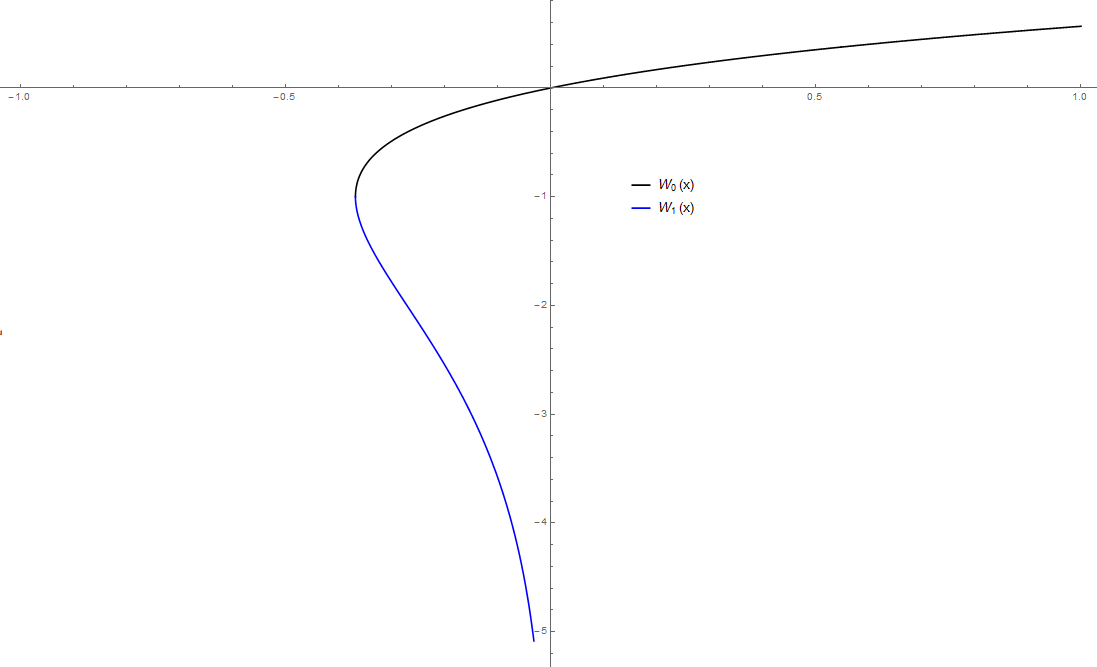
| − | + | The Lambert $W$ function is the (multi-valued) inverse of the function $g(x)=xe^{x}$. The function $g$ is not [[injective]] because [http://www.wolframalpha.com/input/?i=plot+y%3Dxe^x+for+-1%3Cy%3C2 its graph] does not pass the "horizontal line test". Therefore the inverse function is multi-valued and not unique. This yields two branches of the $W$ function. | |
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
| + | File:lambertwplot.png|Graph of branches $W_0(x)$ and $W_1(x)$ on $[-1,1]$. | ||
| + | </gallery> | ||
| + | </div> | ||
=References= | =References= | ||
[http://arxiv.org/pdf/1003.1628.pdf Having fun with the Lambert $W(x)$ function] | [http://arxiv.org/pdf/1003.1628.pdf Having fun with the Lambert $W(x)$ function] | ||
Revision as of 17:19, 19 February 2015
The Lambert $W$ function is the (multi-valued) inverse of the function $g(x)=xe^{x}$. The function $g$ is not injective because its graph does not pass the "horizontal line test". Therefore the inverse function is multi-valued and not unique. This yields two branches of the $W$ function.
Graph of branches $W_0(x)$ and $W_1(x)$ on $[-1,1]$.
