Difference between revisions of "Riemann zeta"
From specialfunctionswiki
(→External links) |
(→External links) |
||
| Line 38: | Line 38: | ||
*[https://www.youtube.com/watch?v=yhtcJPI6AtY The Riemann Hypothesis: How to make $1 Million Without Getting Out of Bed] | *[https://www.youtube.com/watch?v=yhtcJPI6AtY The Riemann Hypothesis: How to make $1 Million Without Getting Out of Bed] | ||
*[http://empslocal.ex.ac.uk/people/staff/mrwatkin//zeta/riemannhyp.htm The Riemann Hypothesis: FAQ and resources] | *[http://empslocal.ex.ac.uk/people/staff/mrwatkin//zeta/riemannhyp.htm The Riemann Hypothesis: FAQ and resources] | ||
| + | *[http://empslocal.ex.ac.uk/people/staff/mrwatkin//zeta/devlin.pdf How Euler discovered the zeta function] | ||
Revision as of 00:12, 21 March 2015
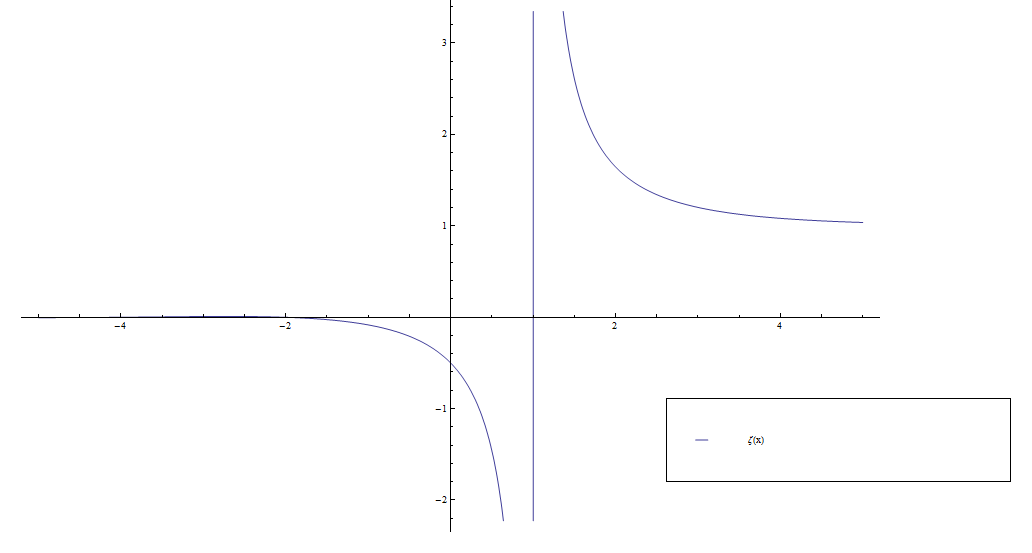
Consider the function $\zeta$ defined by the series $$\zeta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z}.$$
- Complex zeta.jpg
Domain coloring of analytic continuation of $\zeta$.
Properties
Proposition: If $\mathrm{Re} \hspace{2pt} z > 1$, then the series defining $\zeta(z)$ converges.
Proof: █
Proposition (Euler Product): $\zeta(z)=\displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z} = \displaystyle\prod_{p \mathrm{\hspace{2pt} prime}} \dfrac{1}{1-p^{-z}}$
Proof: █
Proposition: Let $n$ be a positive integer. Then $$\zeta(2n)=(-1)^{n+1}\dfrac{B_{2n}(2\pi)^{2n}}{2(2n)!},$$ where $B_n$ denotes the Bernoulli numbers.
Proof: █
External links
- 15 Videos about the Riemann $\zeta$ function
- English translation of Riemann's paper "On the number of prime numbers less than a given quantity"
- Evaluating $\zeta(2)$
- The Riemann Hypothesis: How to make $1 Million Without Getting Out of Bed
- The Riemann Hypothesis: FAQ and resources
- How Euler discovered the zeta function