Difference between revisions of "Sinc"
From specialfunctionswiki
| Line 9: | Line 9: | ||
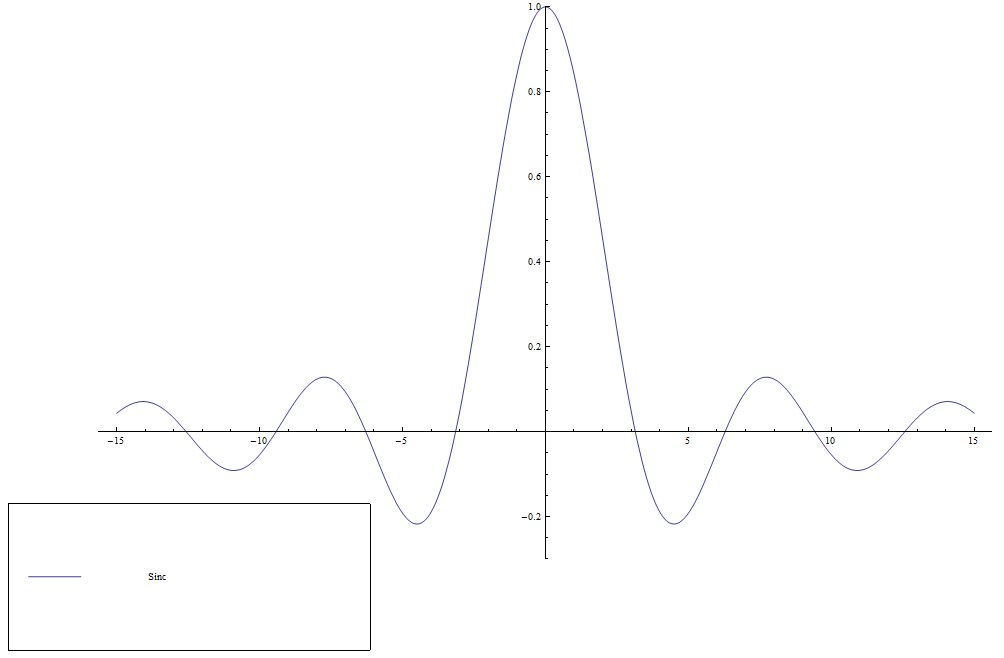
File:Sinc.png|Plot of $\mathrm{sinc}$ on $[-15,15]$. | File:Sinc.png|Plot of $\mathrm{sinc}$ on $[-15,15]$. | ||
</gallery> | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | <div class="toccolours mw-collapsible mw-collapsed"> | ||
| + | <strong>Theorem:</strong> The following formula holds: | ||
| + | $$\mathrm{sin}(x)=\displaystyle\prod_{k=1}^{\infty} \cos \left( \dfrac{x}{2^k} \right).$$ | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <strong>Proof:</strong> █ | ||
| + | </div> | ||
</div> | </div> | ||
=Videos= | =Videos= | ||
[https://www.youtube.com/watch?v=xEFi0xQRCKI Infinite Product Evaluation with the Sinc Function] | [https://www.youtube.com/watch?v=xEFi0xQRCKI Infinite Product Evaluation with the Sinc Function] | ||
Revision as of 02:09, 30 April 2015
The $\mathrm{sinc}$ function is defined by $$\mathrm{sinc}(x) = \left\{ \begin{array}{ll} \dfrac{\sin x}{x} &; x \neq 0 \\ 1 &; x=0. \end{array} \right.$$
Properties
Theorem: The following formula holds: $$\mathrm{sin}(x)=\displaystyle\prod_{k=1}^{\infty} \cos \left( \dfrac{x}{2^k} \right).$$
Proof: █