Difference between revisions of "Bessel Y"
From specialfunctionswiki
| Line 6: | Line 6: | ||
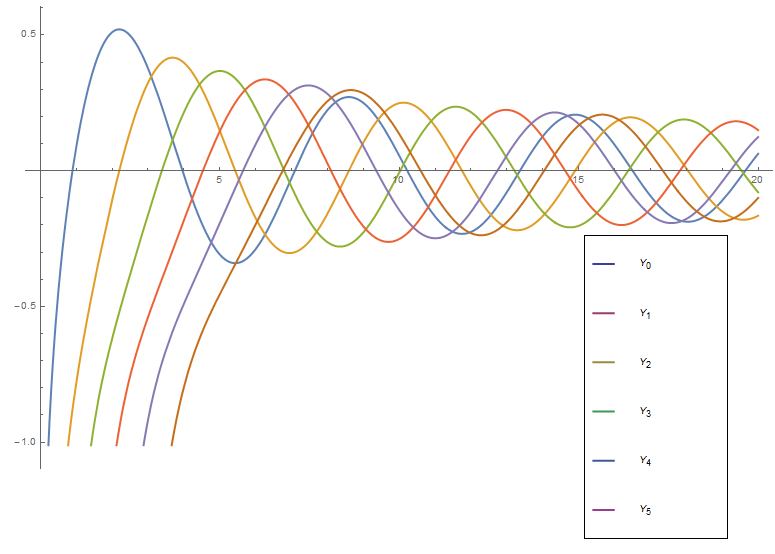
File:Bessel y plot.png|Graph of $Y_0,Y_1,\ldots,Y_5$ on $[0,20]$. | File:Bessel y plot.png|Graph of $Y_0,Y_1,\ldots,Y_5$ on $[0,20]$. | ||
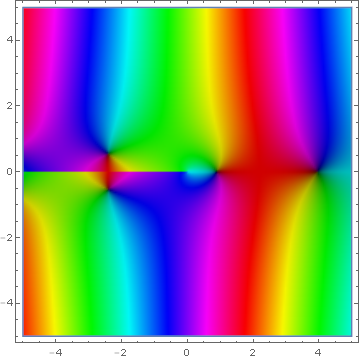
File:Complex bessel y sub 0.png|[[Domain coloring]] of [[analytic continuation]] of $Y_0(z)$. | File:Complex bessel y sub 0.png|[[Domain coloring]] of [[analytic continuation]] of $Y_0(z)$. | ||
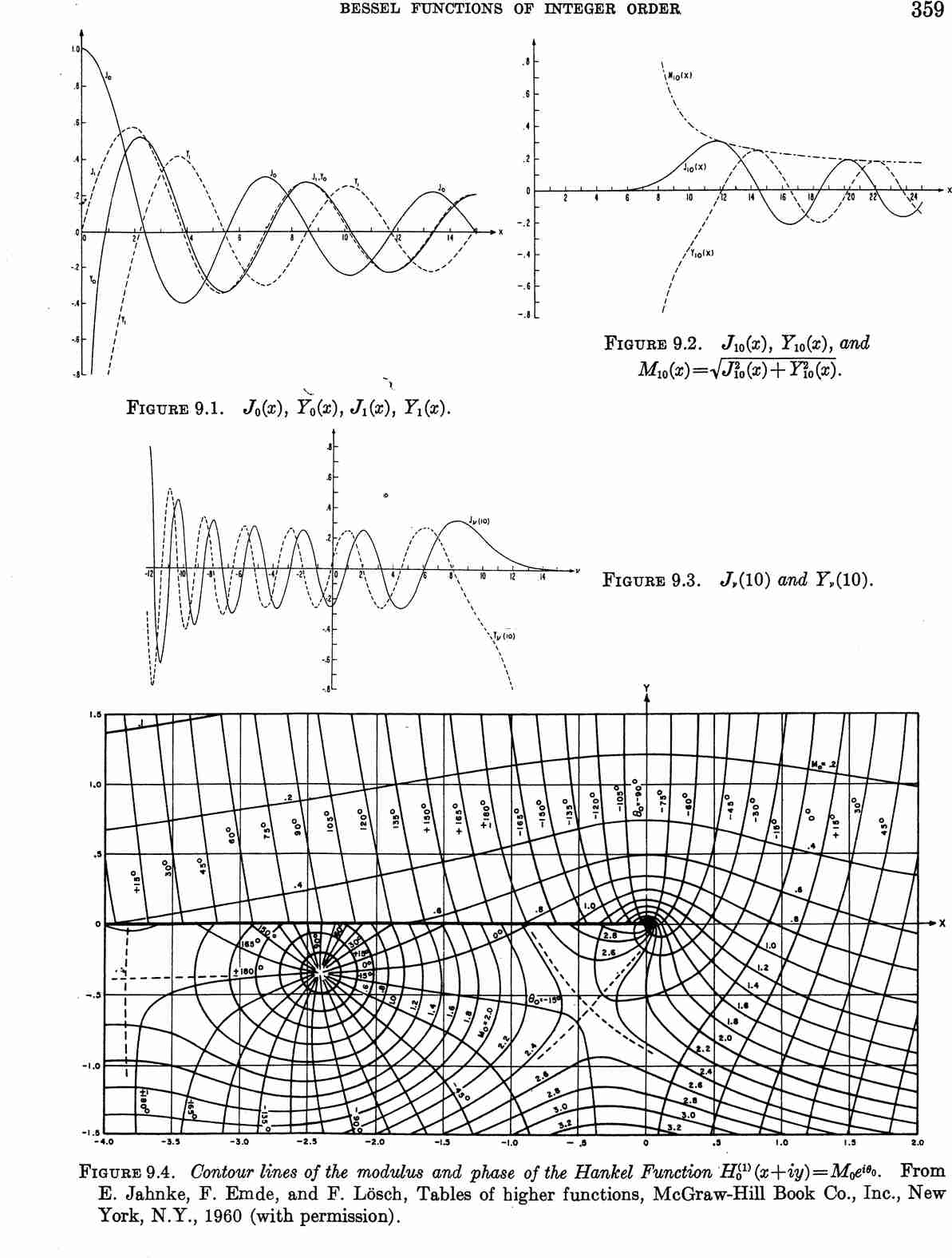
| + | File:Page 359Abramowitz-Stegun(Bessel functions).jpg|Bessel functions from [http://dualaud.net/specialfunctionswiki/abramowitz_and_stegun-1.03/ Abramowitz&Stegun] | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
Revision as of 06:05, 10 June 2015
Bessel functions (of the second kind) $Y_{\nu}$ are defined via the formula $$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$
Domain coloring of analytic continuation of $Y_0(z)$.
Bessel functions from Abramowitz&Stegun