Difference between revisions of "Dirichlet beta"
From specialfunctionswiki
| Line 2: | Line 2: | ||
$$\beta(x) = \displaystyle\sum_{k=0}^{\infty} (-1)^k (2k+1)^{-x} = 2^{-x} \Phi \left(-1,x,\dfrac{1}{2} \right),$$ | $$\beta(x) = \displaystyle\sum_{k=0}^{\infty} (-1)^k (2k+1)^{-x} = 2^{-x} \Phi \left(-1,x,\dfrac{1}{2} \right),$$ | ||
where $\Phi$ denotes the [[Lerch transcendent]]. | where $\Phi$ denotes the [[Lerch transcendent]]. | ||
| + | |||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
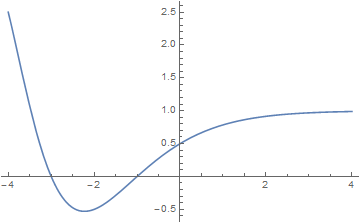
| + | File:Plot dirichlet beta.png|Graph of $\beta$ on $[-4,4]$. | ||
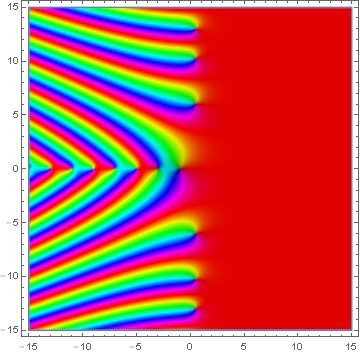
| + | File:Domain coloring dirichlet beta.png|[[Domain coloring]] of [[analytic continuation]] of $\beta$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
{{:Catalan's constant using Dirichlet beta}} | {{:Catalan's constant using Dirichlet beta}} | ||
Revision as of 18:58, 25 July 2015
The Dirichlet $\beta$ function is defined by $$\beta(x) = \displaystyle\sum_{k=0}^{\infty} (-1)^k (2k+1)^{-x} = 2^{-x} \Phi \left(-1,x,\dfrac{1}{2} \right),$$ where $\Phi$ denotes the Lerch transcendent.
Domain coloring of analytic continuation of $\beta$.
Contents
Properties
Theorem
The following formula holds: $$K=\beta(2),$$ where $K$ is Catalan's constant and $\beta$ denotes the Dirichlet beta function.