Difference between revisions of "Error function"
(→Properties) |
|||
| Line 10: | Line 10: | ||
=Properties= | =Properties= | ||
| − | + | {{:Taylor series for error function}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
Revision as of 17:23, 23 May 2016
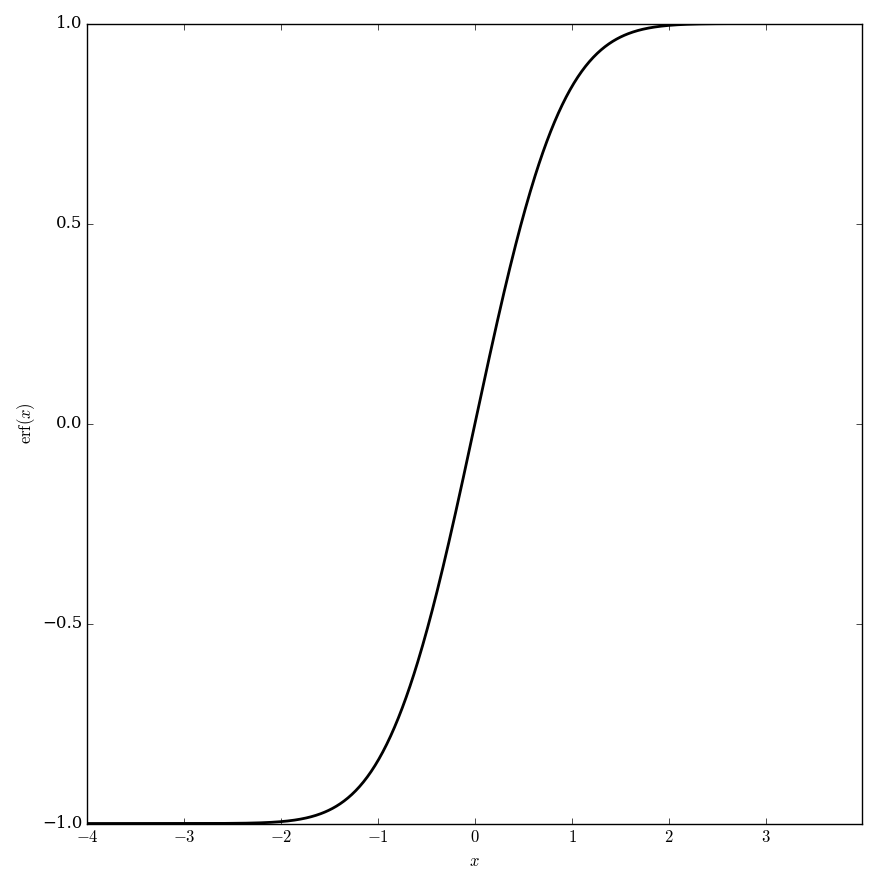
The error function $\mathrm{erf}$ is defined by $$\mathrm{erf}(x)=\dfrac{2}{\sqrt{\pi}}\displaystyle\int_0^x e^{-\tau^2} d\tau.$$
- Complex erf.png
Domain coloring of analytic continuation of $\mathrm{erf}$.
Properties
Theorem
The following formula holds: $$\mathrm{erf}(z) = \dfrac{2}{\sqrt{\pi}} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^kz^{2k+1}}{k!(2k+1)},$$ where $\mathrm{erf}$ denotes the error function and $\pi$ denotes pi, and $k!$ denotes the factorial.
Proof
From the Taylor series of the exponential function, $$e^{-\tau^2}=\displaystyle\sum_{k=0}^{\infty} \dfrac{(-\tau^2)^k}{k!} = \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k \tau^{2k}}{k!}.$$ So, integrating term by term (justify this), $$\displaystyle\int_0^x e^{-\tau^2} \mathrm{d}\tau = \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k \tau^{2k+1}}{k! (2k+1)}.$$ Therefore multiplying by $\dfrac{2}{\sqrt{\pi}}$ and comparing to the definition of the error function, we get $$\mathrm{erf}(z)=\dfrac{2}{\sqrt{\pi}} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k \tau^{2k+1}}{k! (2k+1)},$$ as was to be shown.
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous): $7.1.5$
Theorem: The following formula holds: $\mathrm{erf}(z)=\dfrac{2}{\sqrt{\pi}}e^{-z^2}\displaystyle\sum_{k=0}^{\infty} \dfrac{2^k}{1 \cdot 3 \cdot \ldots \cdot (2k+1)} z^{2k+1}.$
Proof: █
Theorem: The following formula holds:$\mathrm{erf}(-z)=-\mathrm{erf}(z).$
Proof: █
Theorem: The following formula holds:$\mathrm{erf}(\overline{z}) = \overline{\mathrm{erf}}(z).$
Proof: █
Theorem: The following formula holds: $\dfrac{1}{2} \left( 1 + \mathrm{erf} \left( \dfrac{x-\mu}{\sqrt{2}\sigma} \right) \right)=\dfrac{1}{\sigma \sqrt{2 \pi}} \displaystyle\int_{-\infty}^x \exp \left( -\dfrac{(t-\mu)^2}{2\sigma^2} \right)dt.$
Proof: █
Videos
The Laplace transform of the error function $\mathrm{erf}(t)$