Difference between revisions of "Fresnel C"
From specialfunctionswiki
(→Properties) |
|||
| Line 7: | Line 7: | ||
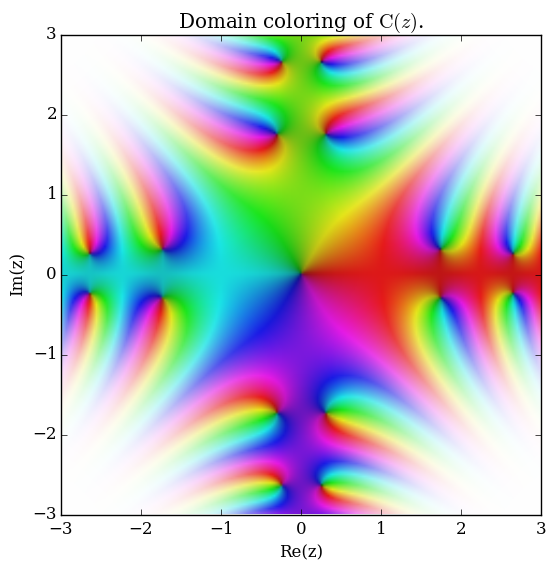
File:Complexfresnelcplot.png|[[Domain coloring]] of Fresnel $C$. | File:Complexfresnelcplot.png|[[Domain coloring]] of Fresnel $C$. | ||
</gallery> | </gallery> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</div> | </div> | ||
Revision as of 22:48, 23 May 2016
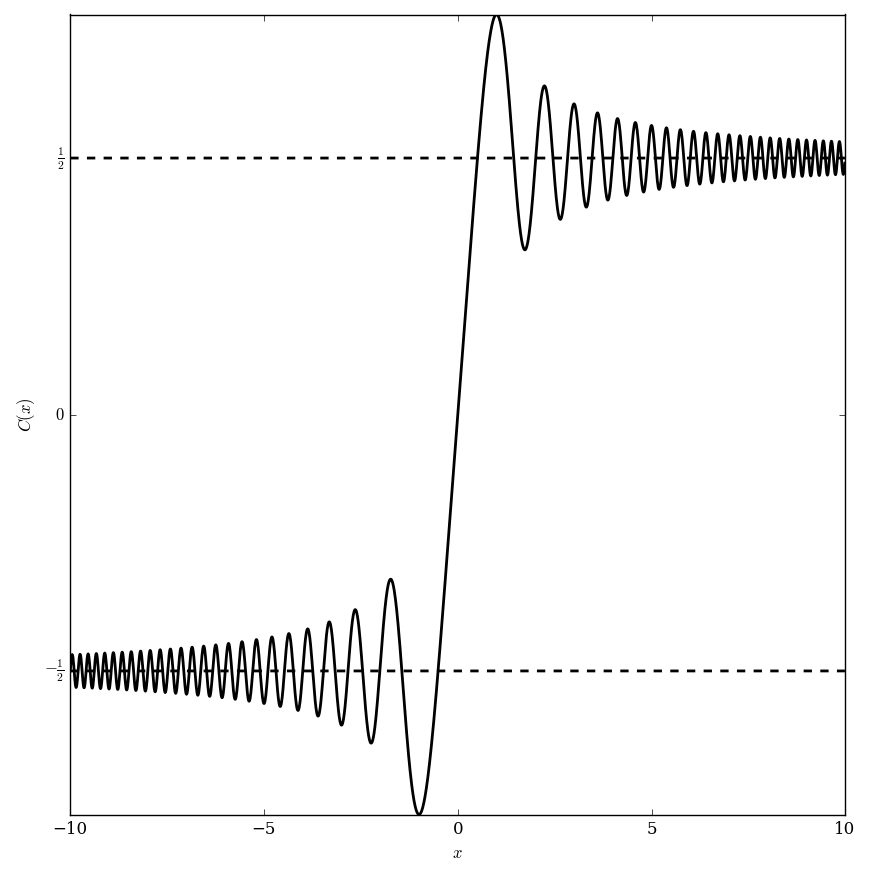
The Fresnel C function is defined by the formula $$C(x)=\int_0^x \cos(t^2) dt.$$ (Note in Abramowitz&Stegun it is defined differently.)
Domain coloring of Fresnel $C$.
See Also
Videos
How to integrate cos(x^2) - The Fresnel Integral C(x)