Difference between revisions of "Barnes G"
| Line 6: | Line 6: | ||
<gallery> | <gallery> | ||
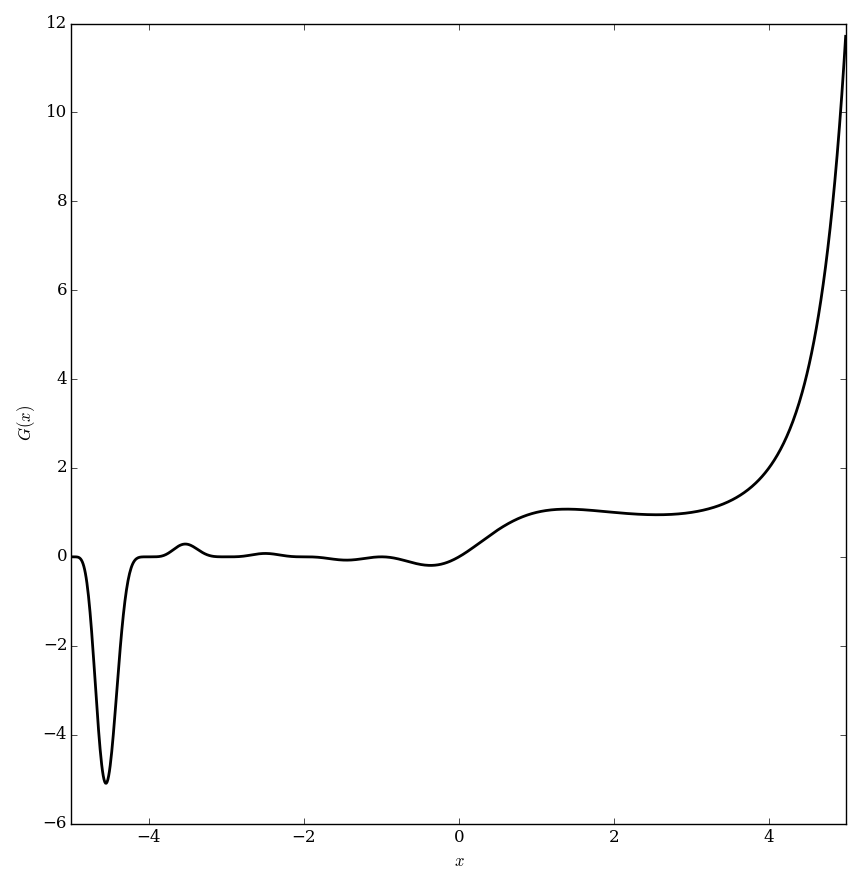
File:Barnesgplot.png|Graph of $G$. | File:Barnesgplot.png|Graph of $G$. | ||
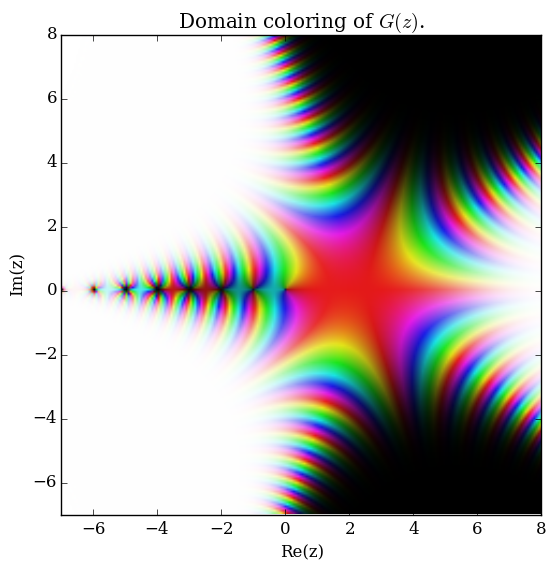
| + | File:Complexbarnesgplot.png|[[Domain coloring]] of $G$. | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
Revision as of 01:19, 24 May 2016
The Barnes $G$ function is defined by the following Weierstrass factorization: $$G(1+z)=(2\pi)^{\frac{z}{2}} \exp \left( - \dfrac{z+z^2(1+\gamma)}{2} \right) \displaystyle\prod_{k=1}^{\infty} \left\{ \left( 1+\dfrac{z}{k} \right)^k \exp \left( \dfrac{z^2}{2k}-z \right) \right\},$$ where $\exp$ denotes the exponential function and $\gamma$ denotes the Euler-Mascheroni constant.
Domain coloring of $G$.
Properties
Theorem
The following formula holds: $$G(z+1)=\Gamma(z)G(z),$$ where $G$ denotes the Barnes G function and $\Gamma$ denotes the gamma function.
Proof
References
Theorem
The following formula holds: $$G(n) = \left\{ \begin{array}{ll} 0&\quad n=-1,-2,\ldots \\ \displaystyle\prod_{k=0}^{n-2} k!&\quad n=0,1,2,\ldots, \end{array} \right.$$ where $G$ denotes the Barnes G function and $i!$ denotes the factorial.