Difference between revisions of "Loggamma"
From specialfunctionswiki
(Created page with "The loggamma function $\log \Gamma$ is defined by the principal branch of $$\log \Gamma(z)=\log(\Gamma(z)),$$ where $\log$ denotes the logarithm and $\Gamma$ denotes t...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
$$\log \Gamma(z)=\log(\Gamma(z)),$$ | $$\log \Gamma(z)=\log(\Gamma(z)),$$ | ||
where $\log$ denotes the [[logarithm]] and $\Gamma$ denotes the [[gamma]] function. | where $\log$ denotes the [[logarithm]] and $\Gamma$ denotes the [[gamma]] function. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
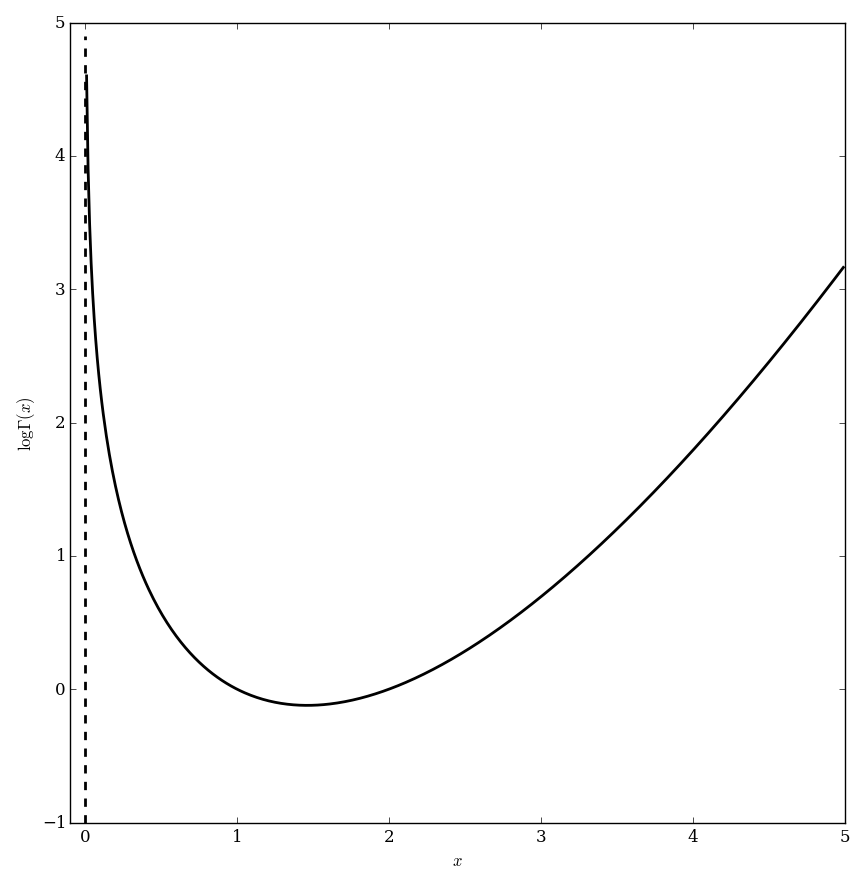
| + | File:Loggammaplot.png|Graph of $\log \Gamma$. | ||
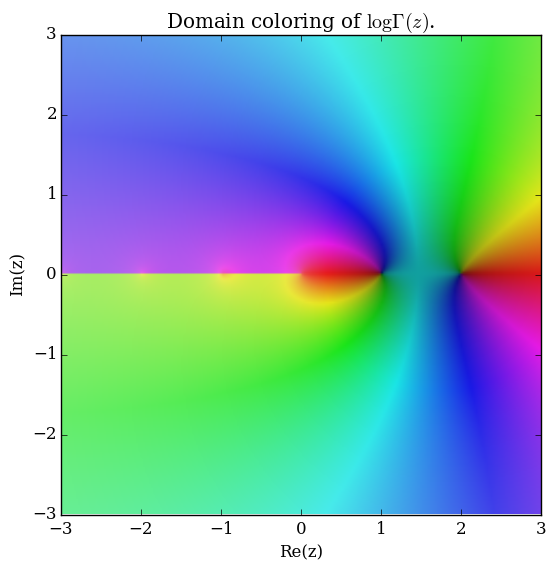
| + | File:Complexloggammaplot.png|[[Domain coloring]] of $\log \Gamma$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =See Also= | ||
| + | [[Gamma]] | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 18:32, 24 May 2016
The loggamma function $\log \Gamma$ is defined by the principal branch of $$\log \Gamma(z)=\log(\Gamma(z)),$$ where $\log$ denotes the logarithm and $\Gamma$ denotes the gamma function.
Domain coloring of $\log \Gamma$.