Difference between revisions of "Riemann Siegel theta function"
From specialfunctionswiki
(Created page with "The Riemann Siegel $\vartheta$ function is defined for $t \in \mathbb{R}$ by $$\vartheta(t) = \mathrm{Im} \left( \log \Gamma \left(\dfrac{1}{4}+ i \dfrac{t}{2} \right) - \dfra...") |
|||
| Line 9: | Line 9: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 18:33, 24 May 2016
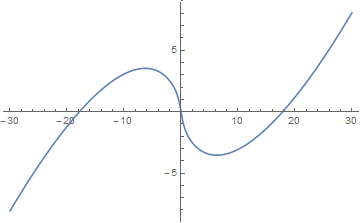
The Riemann Siegel $\vartheta$ function is defined for $t \in \mathbb{R}$ by $$\vartheta(t) = \mathrm{Im} \left( \log \Gamma \left(\dfrac{1}{4}+ i \dfrac{t}{2} \right) - \dfrac{t \log \pi}{2} \right),$$ where $\log$ denotes the logarithm and $\Gamma$ denotes the gamma function.
Graph of $\vartheta$ on $[-30,30]$.
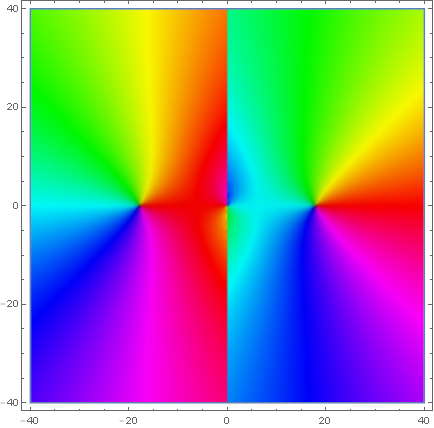
Domain coloring of analytic continuation of $\vartheta$.
