Difference between revisions of "Dilogarithm"
| Line 61: | Line 61: | ||
=References= | =References= | ||
| + | * {{BookReference|Polylogarithms and Associated Functions|1926|ed=2nd|edpage=Second Edition|Leonard Lewin|prev=Inscribing Regular 15-gon in Circle/Corollary|next=Definition:Leading Term}}: page 1 | ||
| + | |||
[http://authors.library.caltech.edu/43491/1/Volume%201.pdf (page 31)]<br /> | [http://authors.library.caltech.edu/43491/1/Volume%201.pdf (page 31)]<br /> | ||
[http://maths.dur.ac.uk/~dma0hg/dilog.pdf The Dilogarithm function]<br /> | [http://maths.dur.ac.uk/~dma0hg/dilog.pdf The Dilogarithm function]<br /> | ||
Revision as of 22:43, 3 June 2016
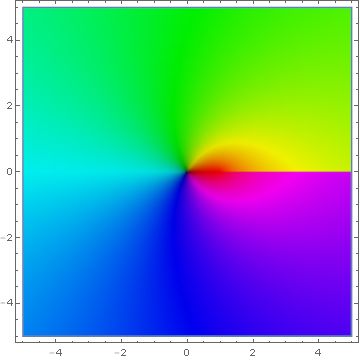
The dilogarithm is the function $$\mathrm{Li}_2(z)=\displaystyle\sum_{k=1}^{\infty} \dfrac{z^k}{k^2}; |z| \leq 1,$$ which is a special case of the polylogarithm.
Domain coloring of analytic continuation of the dilogarithm.
Properties
Theorem: The following formula holds: $$\dfrac{d}{dx} \mathrm{Li}_2 \left( -\dfrac{1}{x} \right) = \dfrac{\log(1+\frac{1}{x})}{x}=\dfrac{\log(1+x)-\log x}{x}.$$
Proof: █
Theorem: The following formula holds: $$\mathrm{Li}_2(z)=-\mathrm{Li}_2 \left( \dfrac{1}{z} \right) - \dfrac{1}{2} \left( \log(z) \right)^2 + \pi i \log(z) + \dfrac{\pi^2}{3}.$$
Proof: █
Theorem: The following formula holds: $$\mathrm{Li}_2(x)+\mathrm{Li}_2(-x)=\dfrac{1}{2}\mathrm{Li}_2(x^2).$$
Proof: █
Theorem: The following formula holds: $$\mathrm{Li}_2(1-x)+\mathrm{Li}_2 \left(1-\dfrac{1}{x} \right)=-\dfrac{1}{2}\left( \log x \right)^2.$$
Proof: █
Theorem: The following formula holds: $$\mathrm{Li}_2(x)+\mathrm{Li}_2(1-x)=\dfrac{\pi^2}{6} - (\log x) \log(1-x).$$
Proof: █
Theorem: The following formula holds: $$\mathrm{Li}_2(-x)-\mathrm{Li}_2(1-x)+\dfrac{1}{2}\mathrm{Li}_2(1-x^2)=-\dfrac{\pi^2}{12} - (\log x) \log(x+1).$$
Proof: █
References
- 1926: Leonard Lewin: Polylogarithms and Associated Functions (2nd ed.) ... (previous) ... (next): page 1