Difference between revisions of "Exponential"
From specialfunctionswiki
| Line 11: | Line 11: | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of the exponential function]]<br /> | |
| − | + | [[Taylor series of the exponential function]]<br /> | |
| − | + | [[Exponential in terms of hypergeometric 0F0]]<br /> | |
| − | + | [[Euler E generating function]]<br /> | |
| + | [[Continued fraction for 1/sqrt(pi) integral from -infinity to infinity of e^(-t^2)/(z-t) dt]]<br /> | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 03:42, 6 June 2016
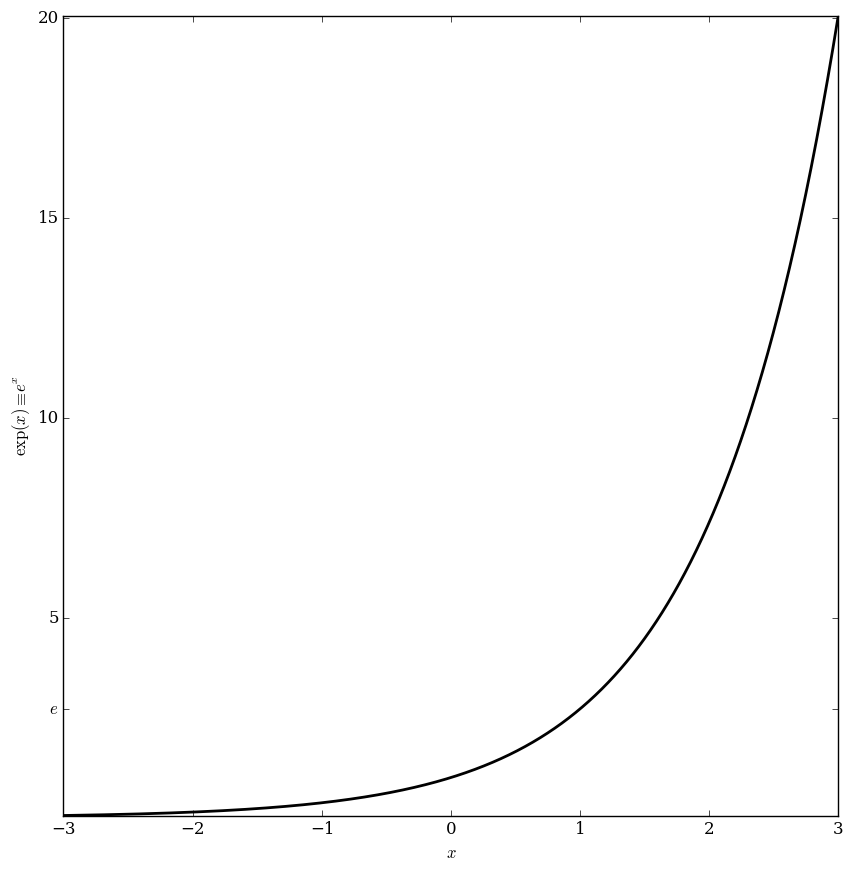
The exponential function $\exp \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula $$\exp(z) = e^z = \sum_{k=0}^{\infty} \dfrac{z^k}{k!},$$ where $e$ is the base of the natural logarithm.
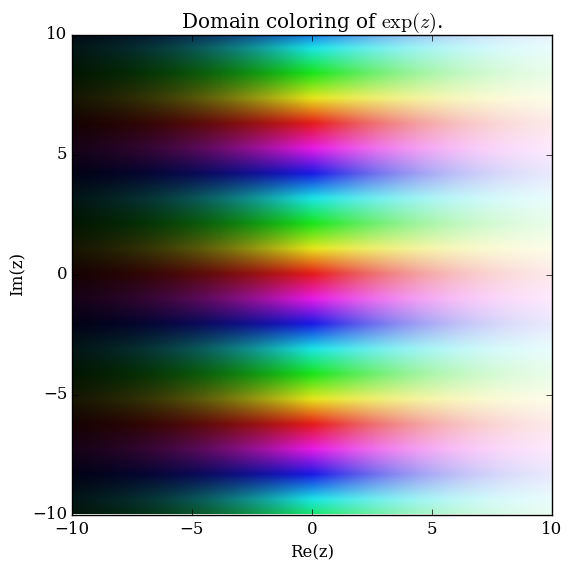
Domain coloring of $\exp$.
Properties
Derivative of the exponential function
Taylor series of the exponential function
Exponential in terms of hypergeometric 0F0
Euler E generating function
Continued fraction for 1/sqrt(pi) integral from -infinity to infinity of e^(-t^2)/(z-t) dt