Difference between revisions of "Barnes G"
From specialfunctionswiki
| (2 intermediate revisions by the same user not shown) | |||
| Line 11: | Line 11: | ||
=Properties= | =Properties= | ||
| − | + | [[Barnes G at z+1 in terms of Barnes G and gamma]]<br /> | |
| − | + | [[Barnes G at positive integer]]<br /> | |
| + | |||
| + | =References= | ||
| + | [http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0031%7CLOG_0022 The theory of the $G$-function by E.W. Barnes] | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
| + | [[Category:Definition]] | ||
Latest revision as of 05:48, 6 June 2016
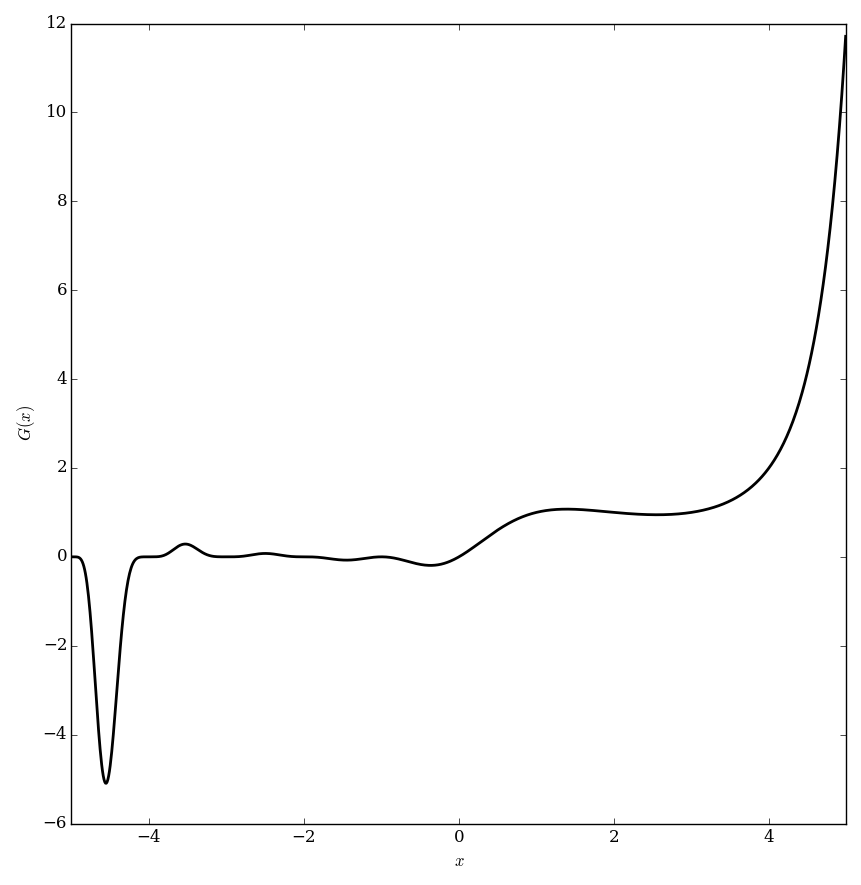
The Barnes $G$ function is defined by the following Weierstrass factorization: $$G(1+z)=(2\pi)^{\frac{z}{2}} \exp \left( - \dfrac{z+z^2(1+\gamma)}{2} \right) \displaystyle\prod_{k=1}^{\infty} \left\{ \left( 1+\dfrac{z}{k} \right)^k \exp \left( \dfrac{z^2}{2k}-z \right) \right\},$$ where $\exp$ denotes the exponential function and $\gamma$ denotes the Euler-Mascheroni constant.
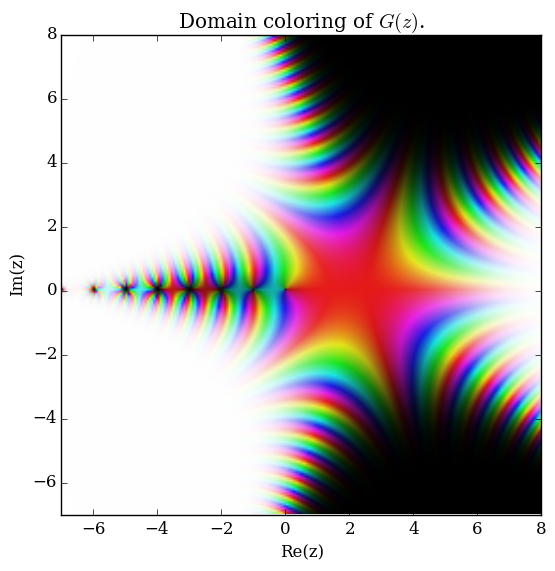
Domain coloring of $G$.
Properties
Barnes G at z+1 in terms of Barnes G and gamma
Barnes G at positive integer