|
|
| Line 15: |
Line 15: |
| | | | |
| | =Properties= | | =Properties= |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem:</strong> The following formula holds for $n \in \mathbb{Z}$:
| |
| − | $$Y_{-n}(z)=(-1)^nY_n(z).$$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| | | | |
| − | {{:Bessel J sub nu and Y sub nu solve Bessel's differential equation}}
| |
| − |
| |
| − | {{:Bessel J sub nu and Y sub nu solve Bessel's differential equation (constant multiple in argument)}}
| |
| − |
| |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem:</strong> The following formula holds for $n\in\mathbb{Z}$:
| |
| − | $${\small Y_n(z)=\dfrac{2}{\pi} \left[ \log \left( \dfrac{z}{2} \right)+\gamma-\dfrac{1}{2}\displaystyle\sum_{k=1}^n \dfrac{1}{k} \right]J_n(x) - \dfrac{1}{\pi} \displaystyle\sum_{k=0}^{\infty} (-1)^k \dfrac{1}{k!(n+k)!} \left(\dfrac{z}{2}\right)^{n+2k}\displaystyle\sum_{j=1}^k \left( \dfrac{1}{j} + \dfrac{1}{j+n} \right) - \dfrac{1}{\pi}\displaystyle\sum_{k=0}^{n-1} \dfrac{(n-k-1)!}{k!} \left( \dfrac{z}{2} \right)^{-n+2k},}$$
| |
| − | where $Y_n$ denotes the [[Bessel Y sub nu|Bessel function of the second kind]], $\log$ denotes the [[logarithm]], $\gamma$ denotes the [[Euler-Mascheroni constant]], and $J_n$ denotes the [[Bessel J sub nu|Bessel function of the first kind]].
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| | | | |
| | =References= | | =References= |
Revision as of 19:55, 9 June 2016
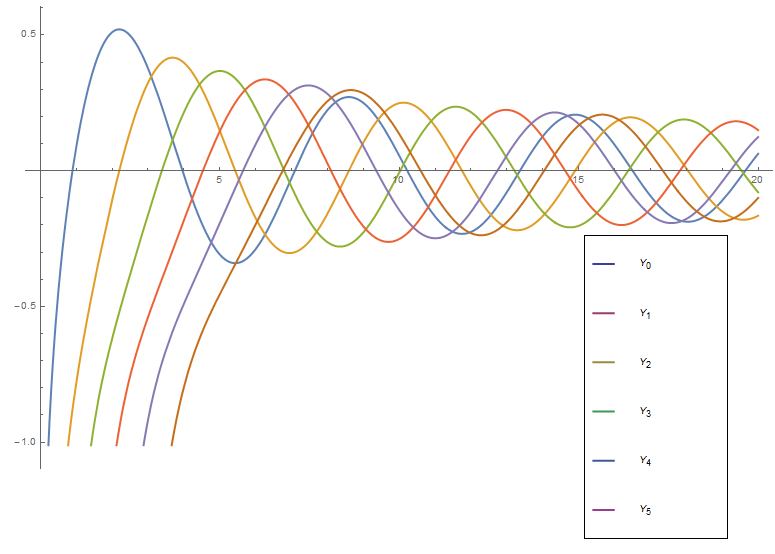
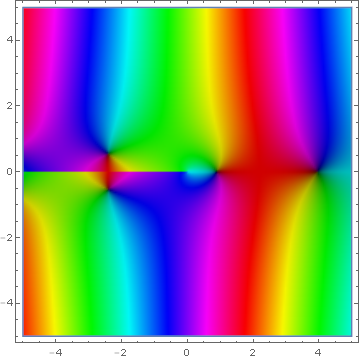
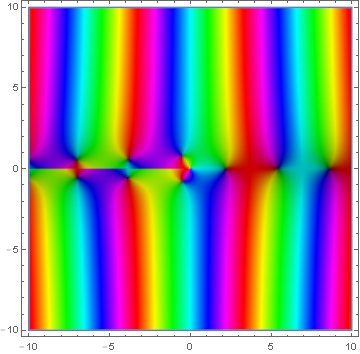
Bessel functions of the second kind $Y_{\nu}$ are defined via the formula
$$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$
Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$.
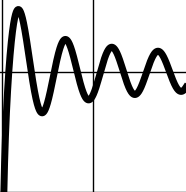
Graph of $Y_0,Y_1,\ldots,Y_5$ on $[0,20]$.
Properties
References
Bessel's functions of the second order - C.V. Coates
<center>Bessel functions
Bessel $Y_{\nu}$ </center>