Difference between revisions of "Spherical Bessel y"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
The spherical Bessel function of the second kind is | The spherical Bessel function of the second kind is | ||
$$y_{\nu}(z)=\sqrt{\dfrac{\pi}{2z}} Y_{\nu+\frac{1}{2}}(z),$$ | $$y_{\nu}(z)=\sqrt{\dfrac{\pi}{2z}} Y_{\nu+\frac{1}{2}}(z),$$ | ||
Revision as of 19:16, 10 June 2016
The spherical Bessel function of the second kind is $$y_{\nu}(z)=\sqrt{\dfrac{\pi}{2z}} Y_{\nu+\frac{1}{2}}(z),$$ where $Y_{\nu}$ denotes the Bessel function of the second kind.
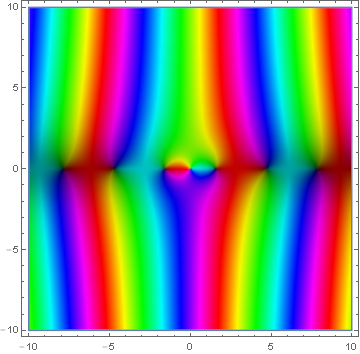
Domain coloring of $y_0$.
Properties
Theorem
The following formula holds for non-negative integers $n$: $$y_n(z)=(-1)^{n+1}z^n \left( \dfrac{1}{z} \dfrac{d}{dz} \right)^n \left( \dfrac{\cos z}{z} \right),$$ where $y_n$ denotes the spherical Bessel function of the second kind and $\cos$ denotes the cosine function.
Proof
References
Spherical Bessel $y_{\nu}$