Difference between revisions of "Bessel Y"
From specialfunctionswiki
| Line 6: | Line 6: | ||
<gallery> | <gallery> | ||
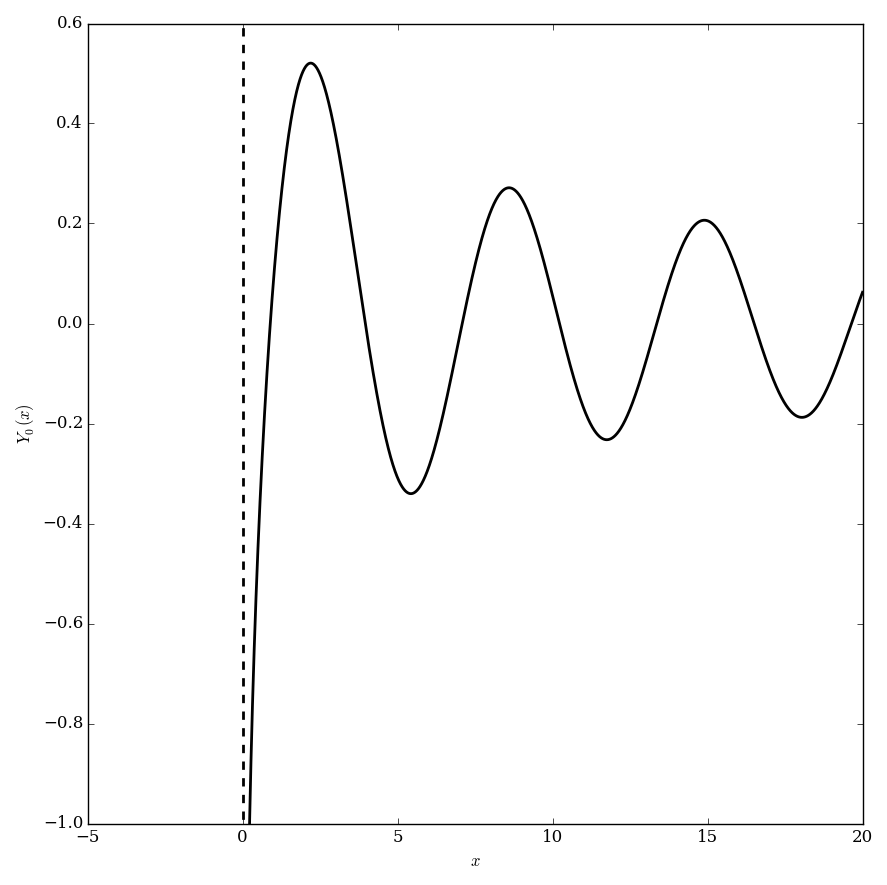
File:Bessely,n=0plot.png|Graph of $Y_0$. | File:Bessely,n=0plot.png|Graph of $Y_0$. | ||
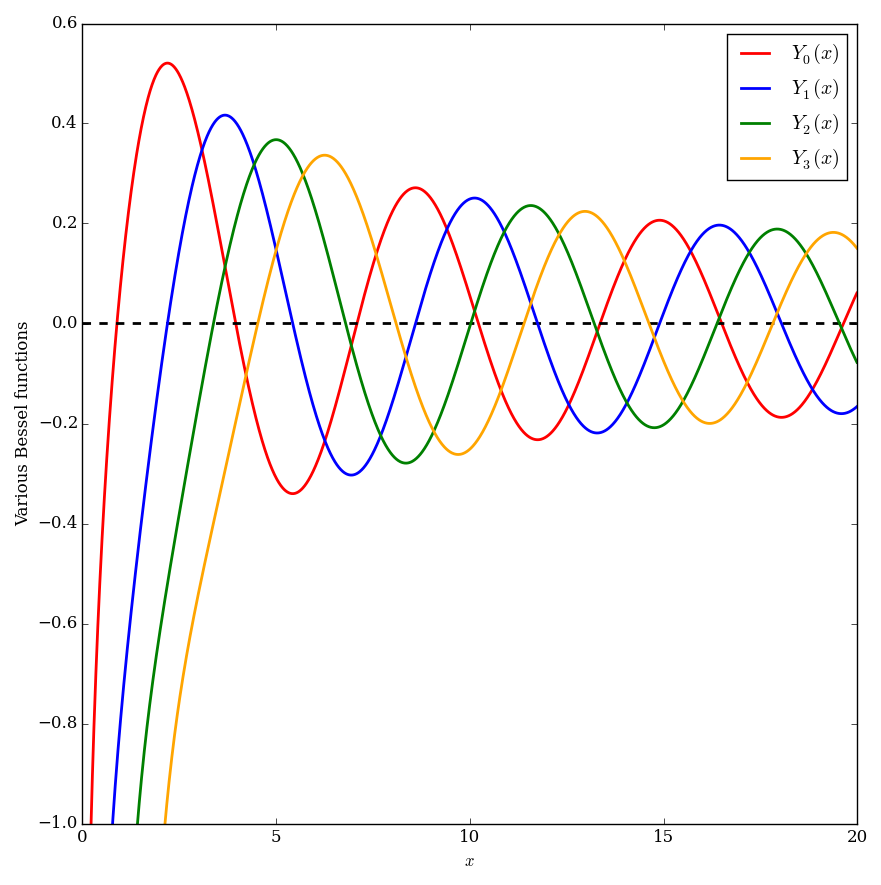
| − | File: | + | File:Multiplebesselyplot.png|Graph of $Y_0,Y_1,\ldots,Y_4$ on $[0,20]$. |
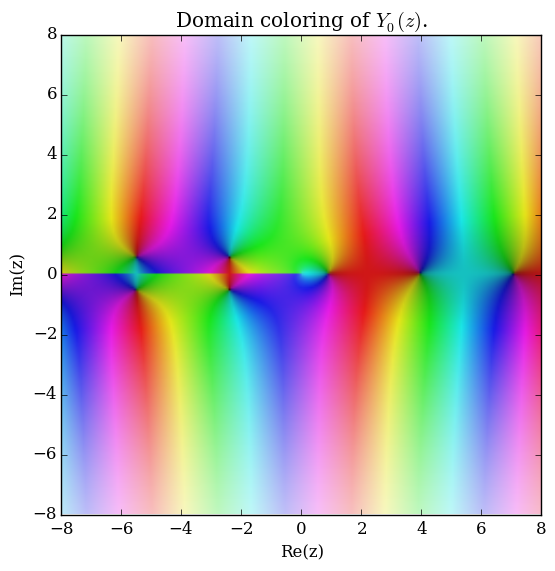
File:Complexbessely,n=0.png|[[Domain coloring]] of $Y_0$. | File:Complexbessely,n=0.png|[[Domain coloring]] of $Y_0$. | ||
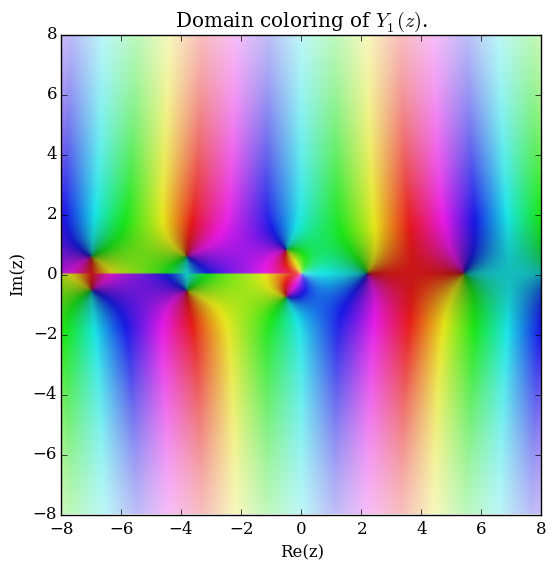
File:Complexbessely,n=1.png|[[Domain coloring]] of $Y_1$. | File:Complexbessely,n=1.png|[[Domain coloring]] of $Y_1$. | ||
Revision as of 19:29, 10 June 2016
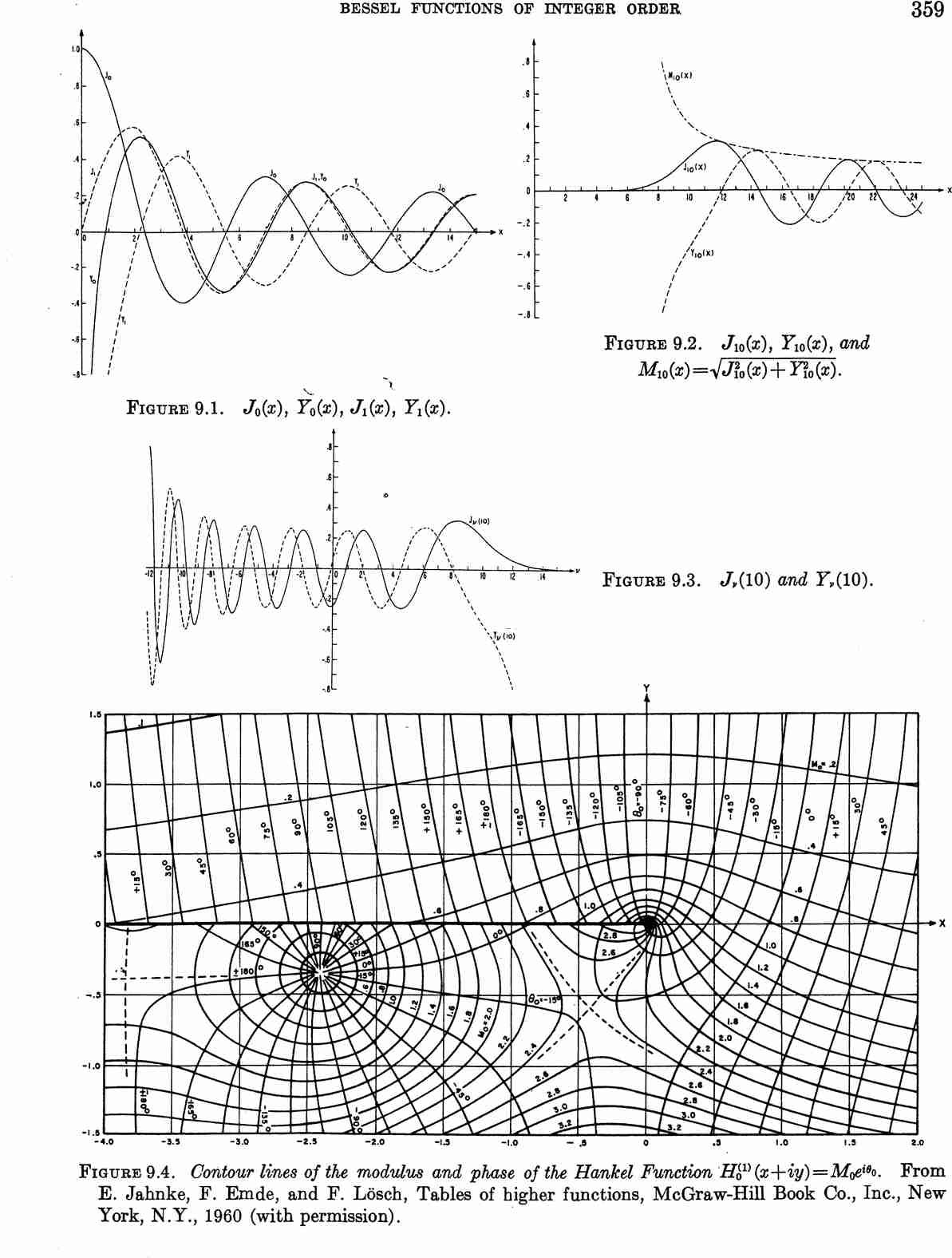
Bessel functions of the second kind $Y_{\nu}$ are defined via the formula $$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$ Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$.
Graph of $Y_0$.
Graph of $Y_0,Y_1,\ldots,Y_4$ on $[0,20]$.
Domain coloring of $Y_0$.
Domain coloring of $Y_1$.
Bessel functions from Abramowitz&Stegun
.jpg)
Properties
References
Bessel's functions of the second order - C.V. Coates
