Difference between revisions of "Fresnel C"
From specialfunctionswiki
| Line 15: | Line 15: | ||
[https://www.youtube.com/watch?v=fR4yd6pB5co How to integrate cos(x^2) - The Fresnel Integral C(x)]<br /> | [https://www.youtube.com/watch?v=fR4yd6pB5co How to integrate cos(x^2) - The Fresnel Integral C(x)]<br /> | ||
| − | + | {{:*-integral functions footer}} | |
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 23:09, 11 June 2016
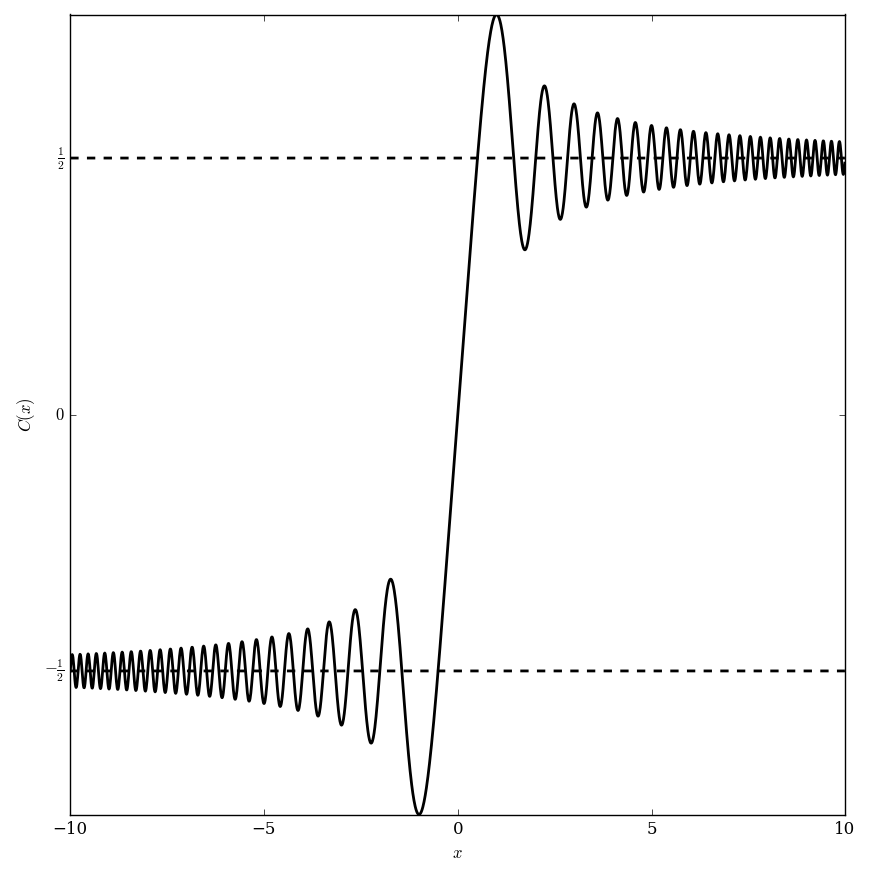
The Fresnel C function is defined by the formula $$C(x)=\int_0^x \cos(t^2) \mathrm{d}t.$$ (Note in Abramowitz&Stegun it is defined differently.)
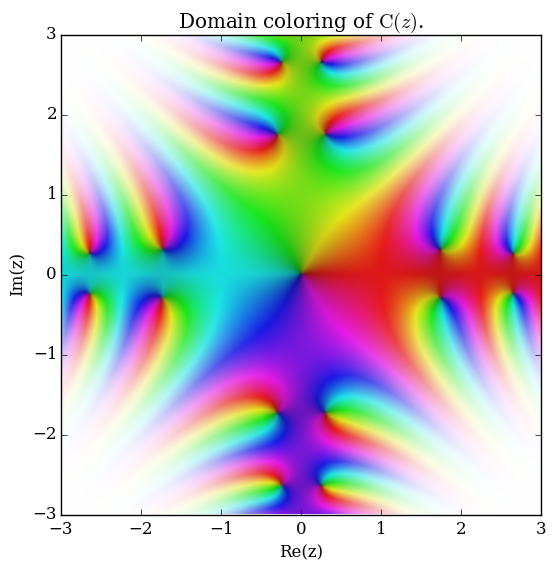
Domain coloring of Fresnel $C$.
See Also
Videos
How to integrate cos(x^2) - The Fresnel Integral C(x)