Difference between revisions of "Logarithmic integral"
From specialfunctionswiki
| Line 17: | Line 17: | ||
[[Prime counting function]] <br /> | [[Prime counting function]] <br /> | ||
| − | + | {{:*-integral functions footer}} | |
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 23:10, 11 June 2016
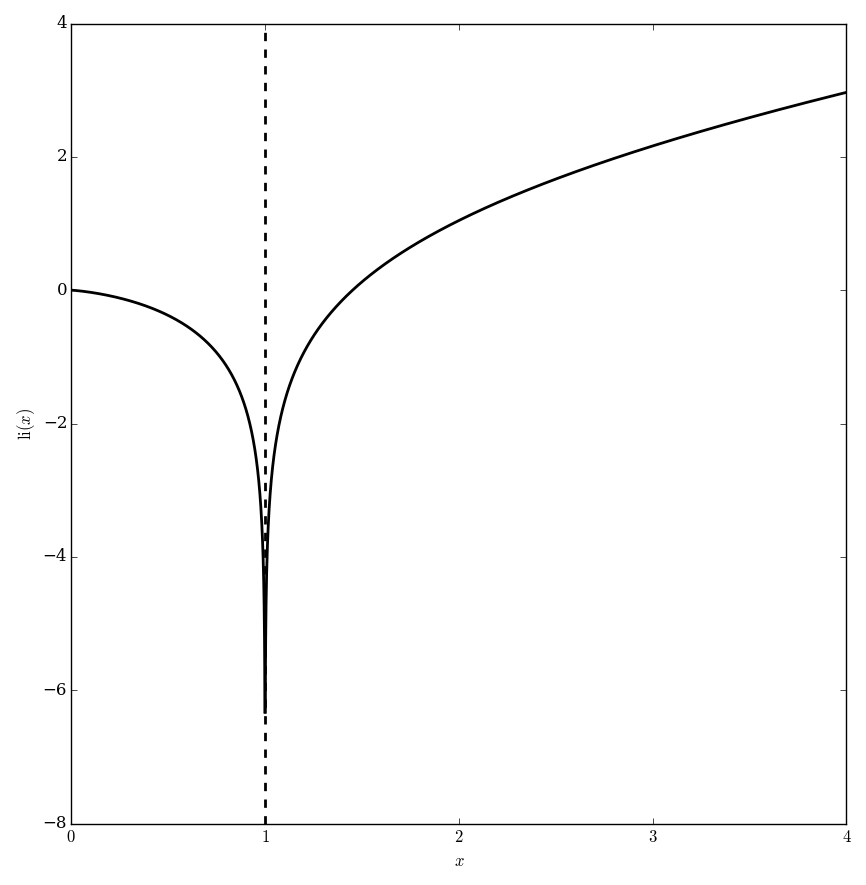
The logarithmic integral is $$\mathrm{li}(x) = \displaystyle\int_0^x \dfrac{1}{\log(t)} \mathrm{d}t,$$ where $\log$ denotes the logarithm.
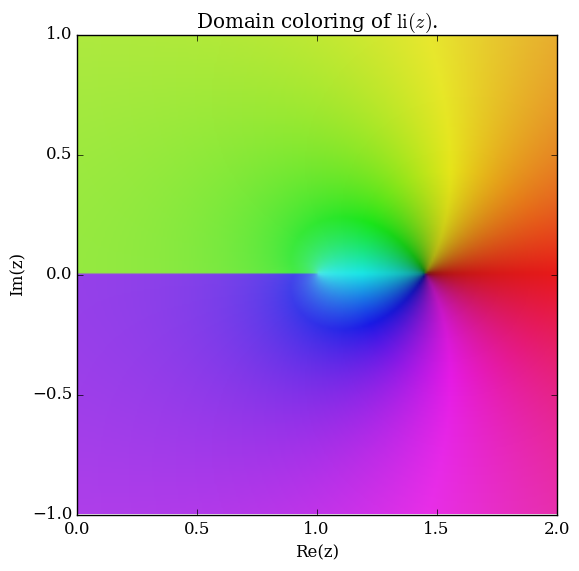
Domain coloring of $\mathrm{li}$.
Properties
Relationship between logarithmic integral and exponential integral
Prime number theorem, logarithmic integral