Difference between revisions of "Spherical Bessel j"
From specialfunctionswiki
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
The spherical Bessel function of the first kind is defined by | The spherical Bessel function of the first kind is defined by | ||
$$j_{\nu}(z)=\sqrt{\dfrac{\pi}{2z}}J_{\nu + \frac{1}{2}}(z),$$ | $$j_{\nu}(z)=\sqrt{\dfrac{\pi}{2z}}J_{\nu + \frac{1}{2}}(z),$$ | ||
| Line 10: | Line 11: | ||
=Properties= | =Properties= | ||
| − | + | [[Relationship between spherical Bessel j sub nu and sine]]<br /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
=References= | =References= | ||
Latest revision as of 22:44, 20 June 2016
The spherical Bessel function of the first kind is defined by $$j_{\nu}(z)=\sqrt{\dfrac{\pi}{2z}}J_{\nu + \frac{1}{2}}(z),$$ where $J_{\nu}$ denotes the Bessel function of the first kind.
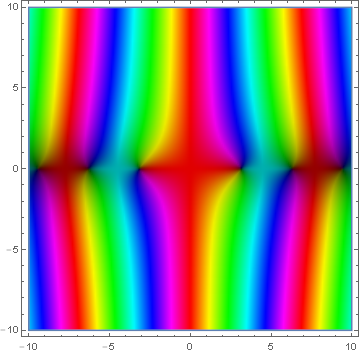
Domain coloring of $j_0$.
Properties
Relationship between spherical Bessel j sub nu and sine
References
Spherical Bessel $j_{\nu}$