Difference between revisions of "Erfc"
From specialfunctionswiki
| Line 13: | Line 13: | ||
* {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Error function|next=findme}}: 7.1.2 | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Error function|next=findme}}: 7.1.2 | ||
| − | + | {{:Error functions footer}} | |
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 21:56, 6 July 2016
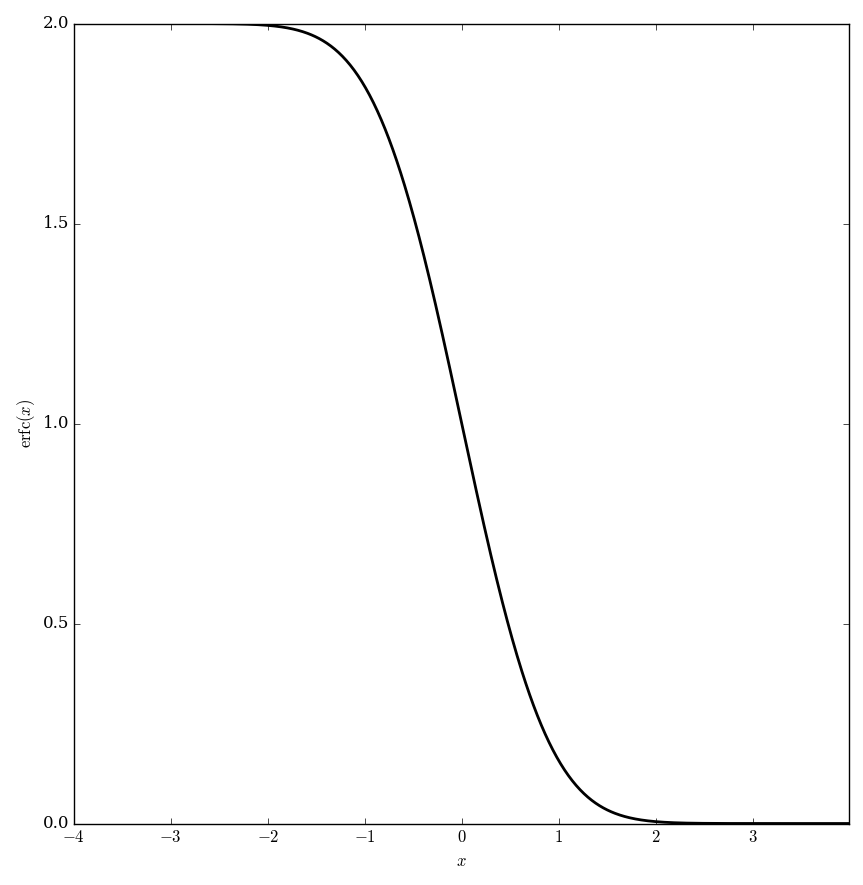
The complementary error function $\mathrm{erfc}$ is defined by the formula $$\mathrm{erfc}(z)=1-\mathrm{erf}(z),$$ where $\mathrm{erf}$ denotes the error function.
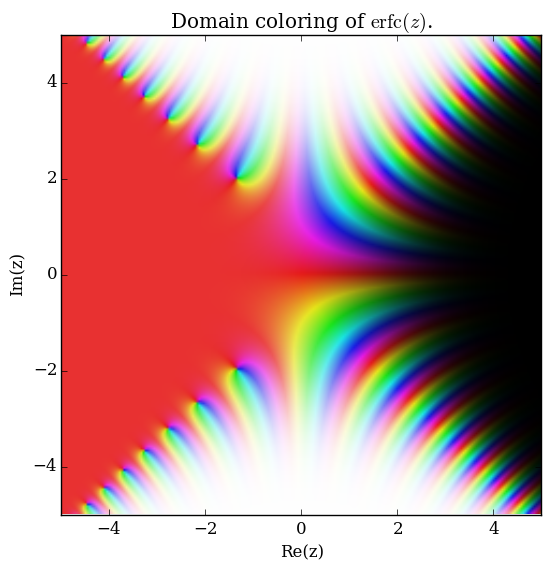
Domain coloring of $\mathrm{erfc}$.
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 7.1.2