Difference between revisions of "Sinc"
From specialfunctionswiki
| (15 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The $\mathrm{sinc}$ function is defined by | + | The $\mathrm{sinc}$ function (sometimes called the "unnormalized" $\mathrm{sinc}$ function) is defined by |
| − | $$\mathrm{sinc}( | + | $$\mathrm{sinc}(z) = \left\{ \begin{array}{ll} |
| − | \dfrac{\sin | + | \dfrac{\sin z}{z} &; z \neq 0 \\ |
| − | 1 &; | + | 1 &; z=0. |
\end{array} \right.$$ | \end{array} \right.$$ | ||
| + | It appears in the definition of the [[Sine integral]] function. | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
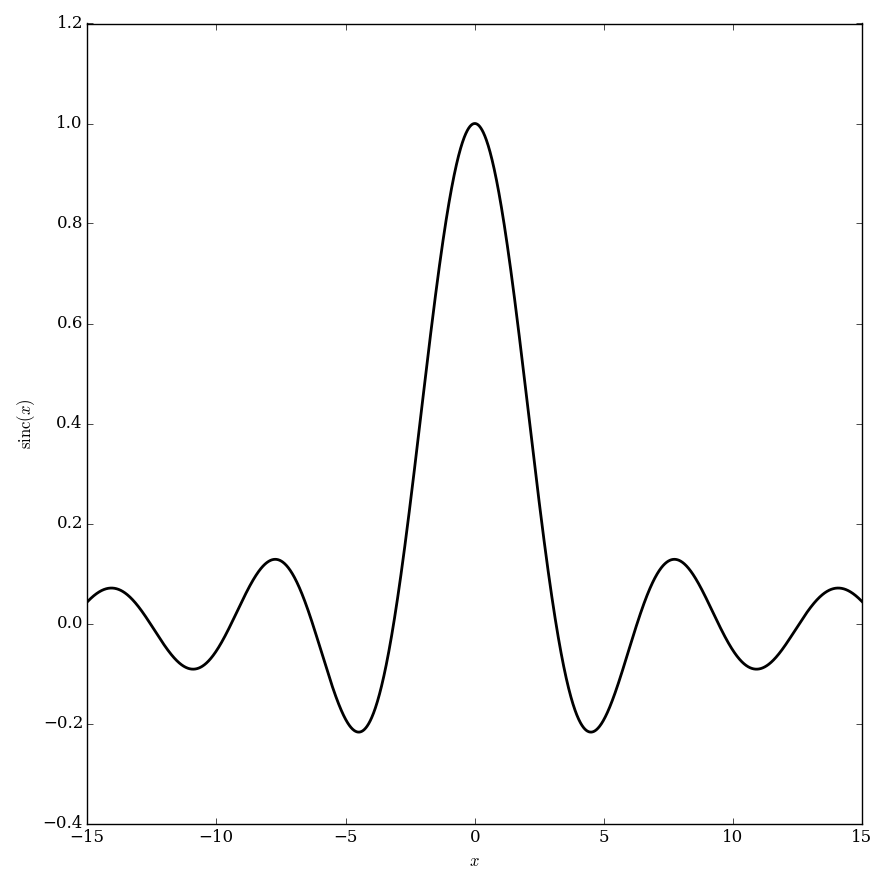
| − | File: | + | File:Sincplot.png|Plot of $\mathrm{sinc}$ on $[-15,15]$. |
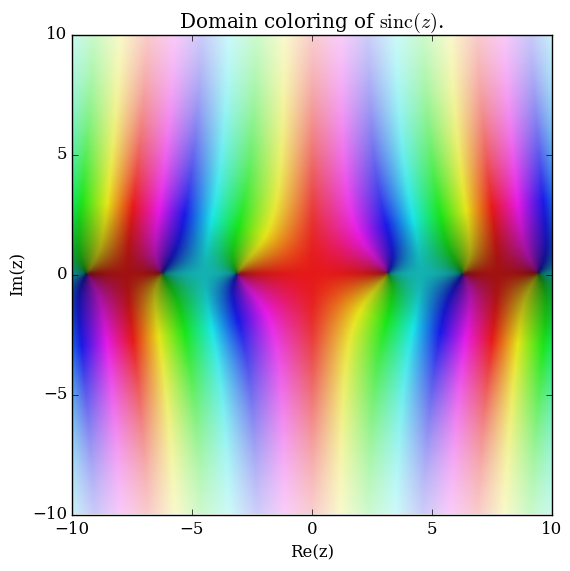
| + | File:Complexsincplot.png|[[Domain coloring]] of $\mathrm{sinc}$. | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[Sum of values of sinc]]<br /> | ||
=Videos= | =Videos= | ||
| − | [https://www.youtube.com/watch?v=xEFi0xQRCKI Infinite Product Evaluation with the Sinc Function] | + | [https://www.youtube.com/watch?v=xEFi0xQRCKI Infinite Product Evaluation with the Sinc Function]<br /> |
| + | [https://www.youtube.com/watch?v=sW9Sw0G8KQ4 (The Sinc Function) Inverse Fourier Transform of Sinc & Fourier Transform of Sinc]<br /> | ||
| + | [https://www.youtube.com/watch?v=ORTQTh4uh7A Fourier Transform of a Sinc Function (or Inverse Fourier Transform of a Low Pass Filter)]<br /> | ||
| + | [https://youtu.be/3Sjn3XLo5XE?t=306 Discrete-Time Signals and Systems Introduction (4/6): Special Functions]<br /> | ||
| + | [https://www.youtube.com/watch?v=xx2AQz_ZyC0 Integrating the sinc function]<br /> | ||
| + | |||
| + | =See also= | ||
| + | [[Normalized sinc]]<br /> | ||
| + | |||
| + | {{:*-c functions footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 02:19, 16 September 2016
The $\mathrm{sinc}$ function (sometimes called the "unnormalized" $\mathrm{sinc}$ function) is defined by $$\mathrm{sinc}(z) = \left\{ \begin{array}{ll} \dfrac{\sin z}{z} &; z \neq 0 \\ 1 &; z=0. \end{array} \right.$$ It appears in the definition of the Sine integral function.
Domain coloring of $\mathrm{sinc}$.
Properties
Videos
Infinite Product Evaluation with the Sinc Function
(The Sinc Function) Inverse Fourier Transform of Sinc & Fourier Transform of Sinc
Fourier Transform of a Sinc Function (or Inverse Fourier Transform of a Low Pass Filter)
Discrete-Time Signals and Systems Introduction (4/6): Special Functions
Integrating the sinc function