Difference between revisions of "Arctan"

From specialfunctionswiki
Jump to: navigation, search
 
(16 intermediate revisions by the same user not shown)
Line 1: Line 1:
 +
__NOTOC__
 
The $\mathrm{arctan}$ function is the inverse function of the [[tangent]] function.<br />
 
The $\mathrm{arctan}$ function is the inverse function of the [[tangent]] function.<br />
  
 
<div align="center">
 
<div align="center">
 
<gallery>
 
<gallery>
−
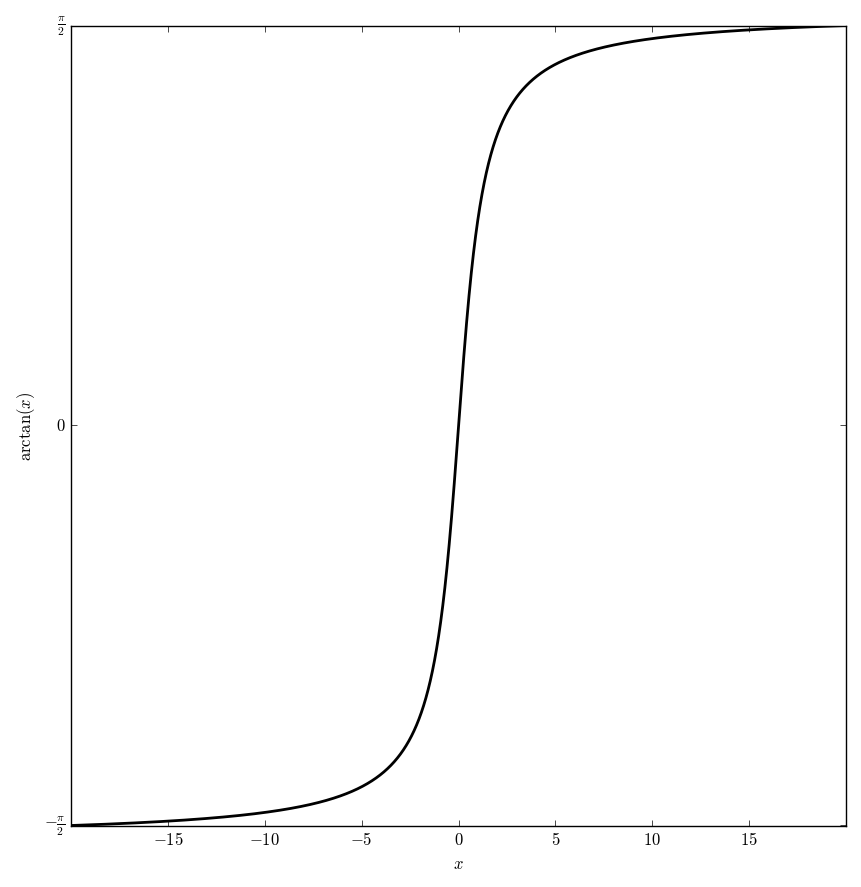
File:Arctan.png|Graph of $\mathrm{arctan}$ on $[-1,1]$.
+
File:Arctanplot.png|Graph of $\mathrm{arctan}$ on $[-20,20]$.
−
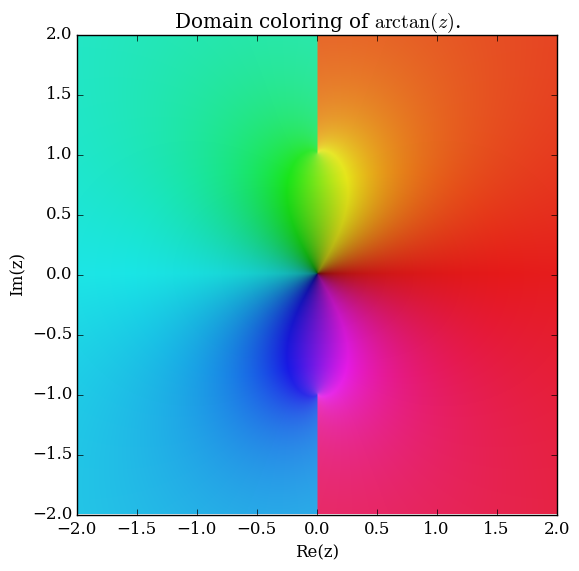
File:Complex arctan.jpg|[[Domain coloring]] of the [[analytic continuation]] of $\mathrm{arctan}$.
+
File:Complexarctanplot.png|[[Domain coloring]] of $\mathrm{arctan}$.
 
</gallery>
 
</gallery>
 
</div>
 
</div>
  
 
=Properties=
 
=Properties=
−
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px">
+
[[Derivative of arctan]]<br />
−
<strong>Proposition:</strong>  
+
[[Antiderivative of arctan]]<br />
−
$$\dfrac{d}{dz} \mathrm{arctan}(z) = \dfrac{1}{z^2+1}$$
+
[[Relationship between arctan and arccot]]<br />
−
<div class="mw-collapsible-content">
+
[[2F1(1/2,1;3/2;-z^2)=arctan(z)/z]]<br />
−
<strong>Proof:</strong> If $\theta=\mathrm{arctan}(z)$ then $\tan \theta = z$. Now use [[implicit differentiation]] with respect to $z$ yields
+
 
−
$$\sec^2(\theta)\theta'=1.$$
+
=References=
−
The following triangle shows that $\sec^2(\mathrm{arctan}(z))=z^2+1$:
+
[http://mathworld.wolfram.com/InverseTangent.html Weisstein, Eric W. "Inverse Tangent." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseTangent.html]
−
[[File:Sec(arctan(z)).png|200px|center]]
 
−
Substituting back in $\theta=\mathrm{arccos(z)}$ yields the formula
 
−
$$\dfrac{d}{dz} \mathrm{arccos(z)} = \dfrac{1}{\sec^2(\mathrm{arctan(z)})} = \dfrac{1}{z^2+1}. █$$
 
−
</div>
 
−
</div>
 
  
−
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px">
+
=See Also=
−
<strong>Proposition:</strong>
+
[[Tangent]] <br />
−
$$\int \mathrm{arctan}(z) = z\mathrm{arctan}(z) - \dfrac{1}{2}\log(1+z^2)+C$$
+
[[Tanh]] <br />
−
<div class="mw-collapsible-content">
+
[[Arctanh]]
−
<strong>Proof:</strong> █
 
−
</div>
 
−
</div>
 
  
−
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px">
+
{{:Inverse trigonometric functions footer}}
−
<strong>Proposition:</strong>
 
−
$$\mathrm{arctan}(z) = \mathrm{arccot}\left( \dfrac{1}{z} \right)$$
 
−
<div class="mw-collapsible-content">
 
−
<strong>Proof:</strong> █
 
−
</div>
 
−
</div>
 
  
−
=References=
+
[[Category:SpecialFunction]]
−
[http://mathworld.wolfram.com/InverseTangent.html Weisstein, Eric W. "Inverse Tangent." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseTangent.html]
 

Latest revision as of 02:46, 16 September 2016

The $\mathrm{arctan}$ function is the inverse function of the tangent function.

  • Graph of $\mathrm{arctan}$ on $[-20,20]$.

  • Domain coloring of $\mathrm{arctan}$.

Properties

Derivative of arctan
Antiderivative of arctan
Relationship between arctan and arccot
2F1(1/2,1;3/2;-z^2)=arctan(z)/z

References

Weisstein, Eric W. "Inverse Tangent." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseTangent.html

See Also

Tangent
Tanh
Arctanh

Inverse trigonometric functions

Arcsin

Arccos

Arctan

Arccsc

Arcsec

Arccot
Retrieved from "http://specialfunctionswiki.org/index.php?title=Arctan&oldid=7437"