Difference between revisions of "Lambert W"
From specialfunctionswiki
| Line 3: | Line 3: | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
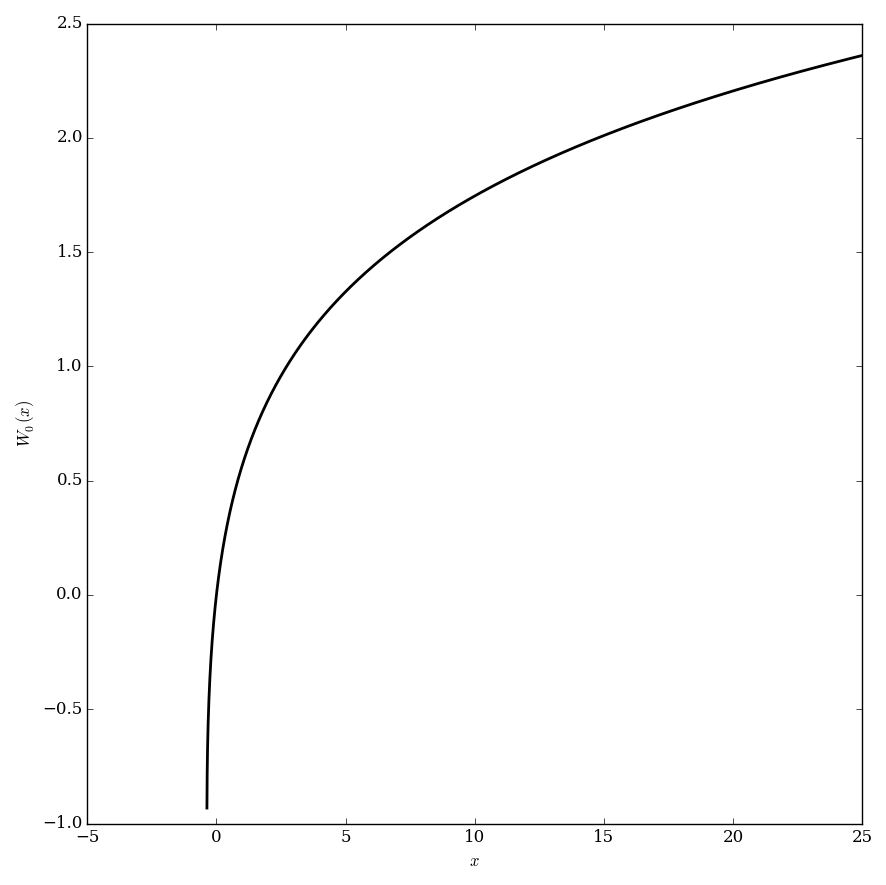
| − | File:Lambertw0plot.png|Plot of the principal branch $W_0 | + | File:Lambertw0plot.png|Plot of the principal branch $W_0$. |
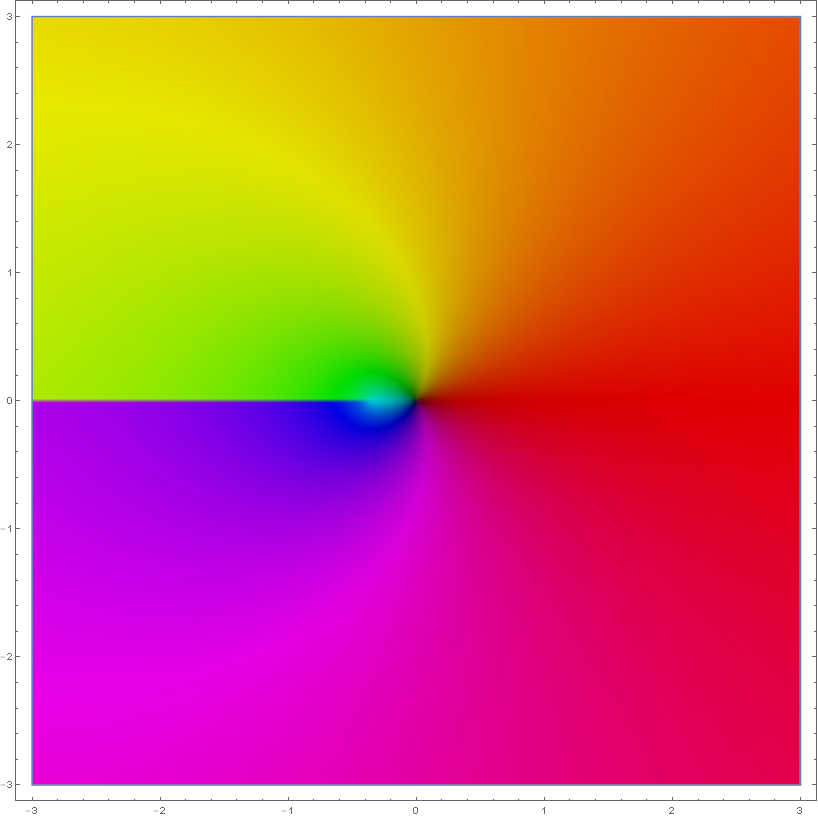
File:Complexlambertw0.png|[[Domain coloring]] of [[analytic continuation]] of branch $W_0(x)$ to $\mathbb{C}$. | File:Complexlambertw0.png|[[Domain coloring]] of [[analytic continuation]] of branch $W_0(x)$ to $\mathbb{C}$. | ||
File:Complexlambertw-1.png|[[Domain coloring]] of [[analytic continuation]] of branch $W_{-1}(x)$ to $\mathbb{C}$. | File:Complexlambertw-1.png|[[Domain coloring]] of [[analytic continuation]] of branch $W_{-1}(x)$ to $\mathbb{C}$. | ||
Revision as of 05:23, 16 September 2016
The Lambert $W$ function is the (multi-valued) inverse of the function $f(x)=xe^{x}$.
Plot of the principal branch $W_0$.
Domain coloring of analytic continuation of branch $W_0(x)$ to $\mathbb{C}$.
Domain coloring of analytic continuation of branch $W_{-1}(x)$ to $\mathbb{C}$.
References
Having fun with the Lambert $W(x)$ function
Videos
6: Recursion, Infinite Tetrations and the Lambert W Function
