Difference between revisions of "Fresnel S"
From specialfunctionswiki
(→Videos) |
|||
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The Fresnel $S$ function is defined by | The Fresnel $S$ function is defined by | ||
| − | $$S( | + | $$S(z)=\int_0^z \sin \left(t^2 \right) \mathrm{d}t.$$ |
| + | (Note in Abramowitz&Stegun it [http://specialfunctionswiki.org/mirror/abramowitz_and_stegun-1.03/page_300.htm is defined] differently.) | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
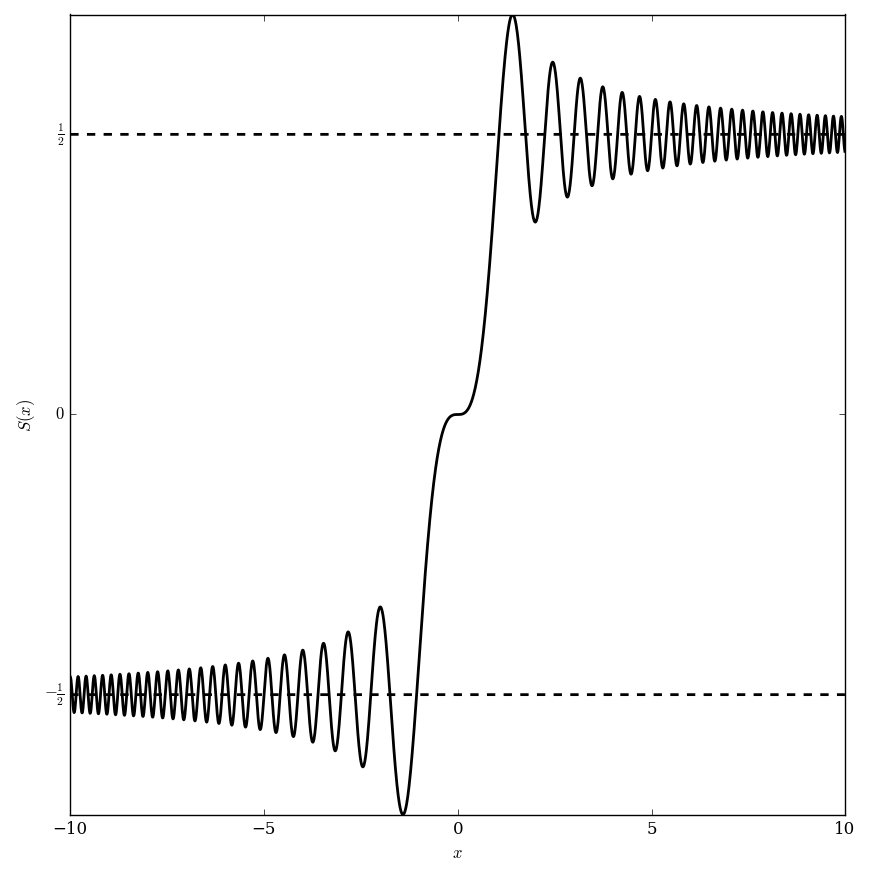
| − | File: | + | File:Fresnelsplot.png| Graph of $S$. |
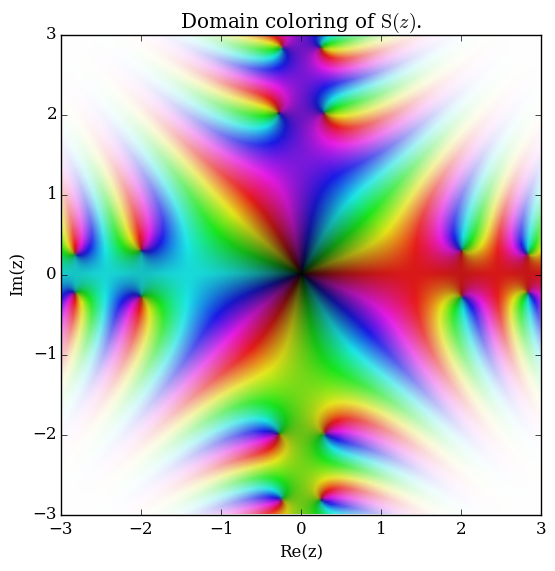
| − | File: | + | File:Complexfresnelsplot.png | [[Domain coloring]] of Fresnel $S$. |
</gallery> | </gallery> | ||
</div> | </div> | ||
=Properties= | =Properties= | ||
| − | < | + | [[Fresnel S is odd]] <br /> |
| − | + | [[Taylor series for Fresnel S]]<br /> | |
| − | + | [[Fresnel S in terms of erf]]<br /> | |
| − | + | [[Limiting value of Fresnel S]]<br /> | |
| − | |||
| − | </ | ||
| − | </ | ||
=See Also= | =See Also= | ||
| Line 22: | Line 20: | ||
=Videos= | =Videos= | ||
| − | [https://www.youtube.com/watch?v=fFZ6BsH99-0 The Fresnel Integral S(x) - How to integrate sin(x^2)]<br /> | + | [https://www.youtube.com/watch?v=fFZ6BsH99-0 The Fresnel Integral S(x) - How to integrate sin(x^2) (12 February 2015)]<br /> |
| + | [https://www.youtube.com/watch?v=H3uOq7VujYA Math and Physics: The Fresnel Integrals (12 May 2016)] <br /> | ||
| + | {{:*-integral functions footer}} | ||
| − | + | [[Category:SpecialFunction]] | |
Latest revision as of 17:21, 5 October 2016
The Fresnel $S$ function is defined by $$S(z)=\int_0^z \sin \left(t^2 \right) \mathrm{d}t.$$ (Note in Abramowitz&Stegun it is defined differently.)
Domain coloring of Fresnel $S$.
Properties
Fresnel S is odd
Taylor series for Fresnel S
Fresnel S in terms of erf
Limiting value of Fresnel S
See Also
Videos
The Fresnel Integral S(x) - How to integrate sin(x^2) (12 February 2015)
Math and Physics: The Fresnel Integrals (12 May 2016)