Difference between revisions of "Arccos"

From specialfunctionswiki
Jump to: navigation, search
 
(24 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
The function $\mathrm{arccos} \colon [-1,1] \longrightarrow [0,\pi]$ is the inverse function of the [[cosine]] function.
+
__NOTOC__
 +
The function $\mathrm{arccos} \colon \mathbb{C} \setminus \{(-\infty,-1) \bigcup (1,\infty) \} \rightarrow \mathbb{C}$ is defined by
 +
$$\rm{arccos}(z)=\dfrac{\pi}{2} + i\log\left( iz + \sqrt{1-z^2} \right),$$
 +
where $i$ denotes the [[imaginary number]] and $\log$ denotes the [[logarithm]].
  
−
[[File:Arccos.png|500px]]
+
<div align="center">
 +
<gallery>
 +
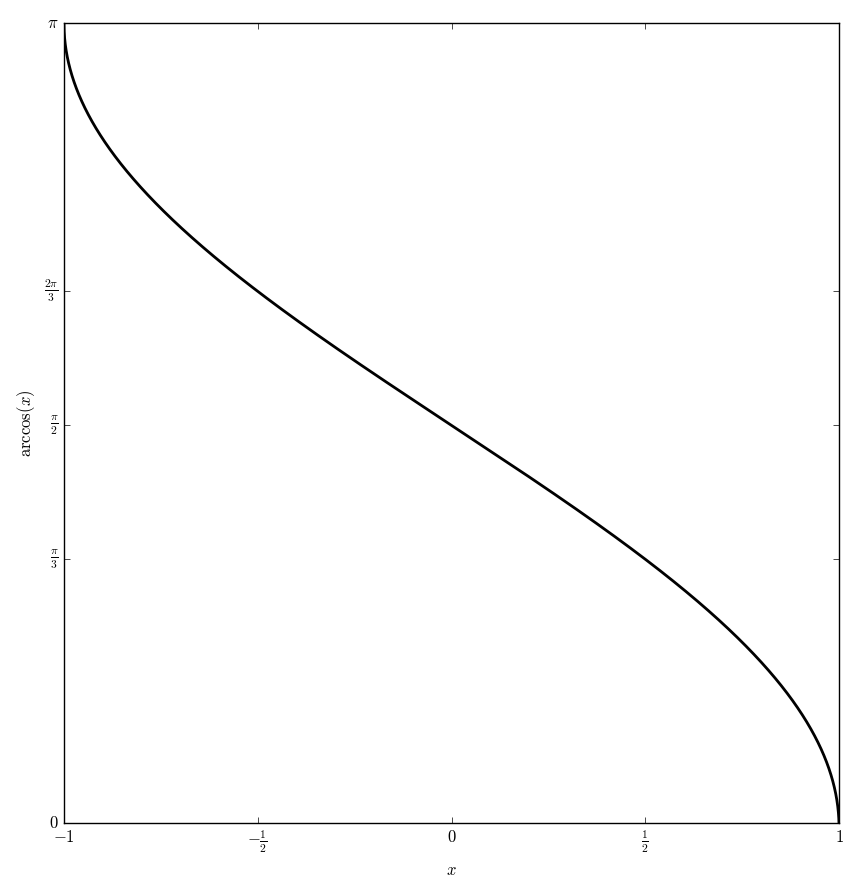
File:Arccosplot.png|Graph of $\mathrm{arccos}$ on $[-1,1]$.
 +
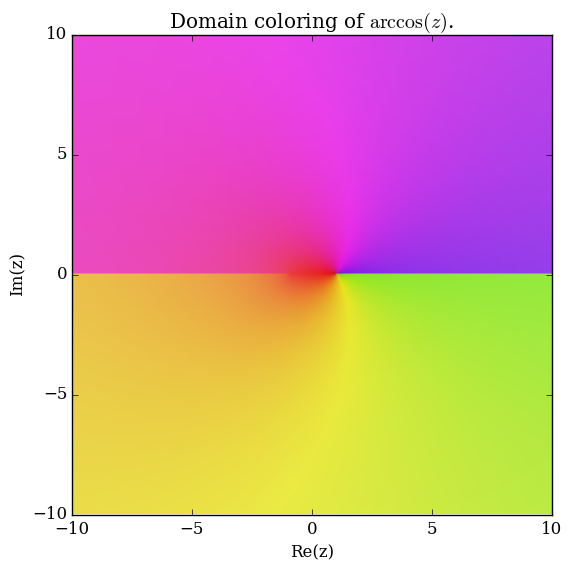
File:Complexarccosplot.png|[[Domain coloring]] of $\mathrm{arccos}$.
 +
</gallery>
 +
</div>
  
−
[[File:Complex arccos.jpg|500px]]
+
=Properties=
 +
[[Arccos as inverse cosine]]<br />
 +
[[Derivative of arccos]]<br />
 +
[[Antiderivative of arccos]]<br />
  
−
=Properties=
+
=References=
−
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px">
+
[http://mathworld.wolfram.com/InverseCosine.html  Weisstein, Eric W. "Inverse Cosine." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseCosine.html]
−
<strong>Proposition:</strong>
 
−
$$\dfrac{d}{dz} \mathrm{arccos}(z) = -\dfrac{1}{\sqrt{1-z^2}}$$
 
−
<div class="mw-collapsible-content">
 
−
<strong>Proof:</strong> If $y=\mathrm{arccos}(z)$ then $\cos(y)=z$. Now use [[implicit differentiation]] with respect to $z$ to get
 
−
$$-\sin(y)y'=1.$$
 
−
Substituting back in $y=\mathrm{arccos}(z)$ yields the formula
 
−
$$\dfrac{d}{dz} \mathrm{arccos}(z) = -\dfrac{1}{\sin(\mathrm{arccos}(z))} = -\dfrac{1}{\sqrt{1-z^2}}.█$$ 
 
−
</div>
 
−
</div>
 
  
−
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px">
+
=See Also=
−
<strong>Proposition:</strong>
+
[[Cosine]] <br />
−
$$\int \mathrm{arccos}(z) dz = z\mathrm{arccos}(z)-\sqrt{1-z^2}+C$$
+
[[Cosh]] <br />
−
<div class="mw-collapsible-content">
+
[[Arccosh]]
−
<strong>Proof:</strong> █
 
−
</div>
 
−
</div>
 
  
−
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px">
+
{{:Inverse trigonometric functions footer}}
−
<strong>Proposition:</strong>
 
−
$$\mathrm{arccos}(z)=\mathrm{arcsec} \left( \dfrac{1}{z} \right)$$
 
−
<div class="mw-collapsible-content">
 
−
<strong>Proof:</strong> █
 
−
</div>
 
−
</div>
 
  
−
=References=
+
[[Category:SpecialFunction]]
−
[http://mathworld.wolfram.com/InverseCosine.html  Weisstein, Eric W. "Inverse Cosine." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseCosine.html]
 

Latest revision as of 20:04, 22 November 2016

The function $\mathrm{arccos} \colon \mathbb{C} \setminus \{(-\infty,-1) \bigcup (1,\infty) \} \rightarrow \mathbb{C}$ is defined by $$\rm{arccos}(z)=\dfrac{\pi}{2} + i\log\left( iz + \sqrt{1-z^2} \right),$$ where $i$ denotes the imaginary number and $\log$ denotes the logarithm.

  • Graph of $\mathrm{arccos}$ on $[-1,1]$.

  • Domain coloring of $\mathrm{arccos}$.

Properties

Arccos as inverse cosine
Derivative of arccos
Antiderivative of arccos

References

Weisstein, Eric W. "Inverse Cosine." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseCosine.html

See Also

Cosine
Cosh
Arccosh

Inverse trigonometric functions

Arcsin

Arccos

Arctan

Arccsc

Arcsec

Arccot
Retrieved from "http://specialfunctionswiki.org/index.php?title=Arccos&oldid=7701"