Difference between revisions of "Derivative of arcsin"
From specialfunctionswiki
(→Proof) |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
==Proof== | ==Proof== | ||
| − | If $\theta=\mathrm{arcsin}(z)$ then $\sin(\theta)=z$. Now use [[implicit differentiation]] with respect to $z$ to get | + | If $\theta=\mathrm{arcsin}(z)$ then $\sin(\theta)=z$. Now use [[implicit differentiation]] with respect to $z$ and the [[derivative of sine]] to get |
| − | $$\cos(\theta)\theta'=1.$$ | + | $$\cos(\theta)\theta'=1,$$ |
| + | or equivalently | ||
| + | $$\dfrac{\mathrm{d}\theta}{\mathrm{d}z} = \dfrac{1}{\cos(\theta)}.$$ | ||
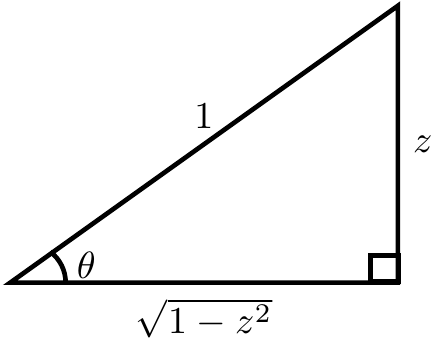
The following image shows that $\cos(\mathrm{arcsin}(z))=\sqrt{1-z^2}$: | The following image shows that $\cos(\mathrm{arcsin}(z))=\sqrt{1-z^2}$: | ||
[[File:Cos(arcsin(z)).png|200px|center]] | [[File:Cos(arcsin(z)).png|200px|center]] | ||
| Line 16: | Line 18: | ||
[[Category:Theorem]] | [[Category:Theorem]] | ||
| + | [[Category:Proven]] | ||
Latest revision as of 23:33, 8 December 2016
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arcsin(z)} = \dfrac{1}{\sqrt{1-z^2}},$$ where $\arcsin$ denotes the inverse sine function.
Proof
If $\theta=\mathrm{arcsin}(z)$ then $\sin(\theta)=z$. Now use implicit differentiation with respect to $z$ and the derivative of sine to get $$\cos(\theta)\theta'=1,$$ or equivalently $$\dfrac{\mathrm{d}\theta}{\mathrm{d}z} = \dfrac{1}{\cos(\theta)}.$$ The following image shows that $\cos(\mathrm{arcsin}(z))=\sqrt{1-z^2}$:
Hence substituting back in $\theta=\mathrm{arccos}(z)$ yields the formula $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arcsin(z)} = \dfrac{1}{\cos(\mathrm{arcsin(z)})} = \dfrac{1}{\sqrt{1-z^2}},$$ as was to be shown. █