Difference between revisions of "Thomae function"
(→Videos) |
|||
| Line 15: | Line 15: | ||
=Properties= | =Properties= | ||
| − | + | [[Thomae function is continuous at irrationals]]<br /> | |
| − | + | [[Thomae function is discontinuous at rationals]]<br /> | |
| − | |||
| − | |||
| − | |||
| − | </ | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
Revision as of 00:34, 9 December 2016
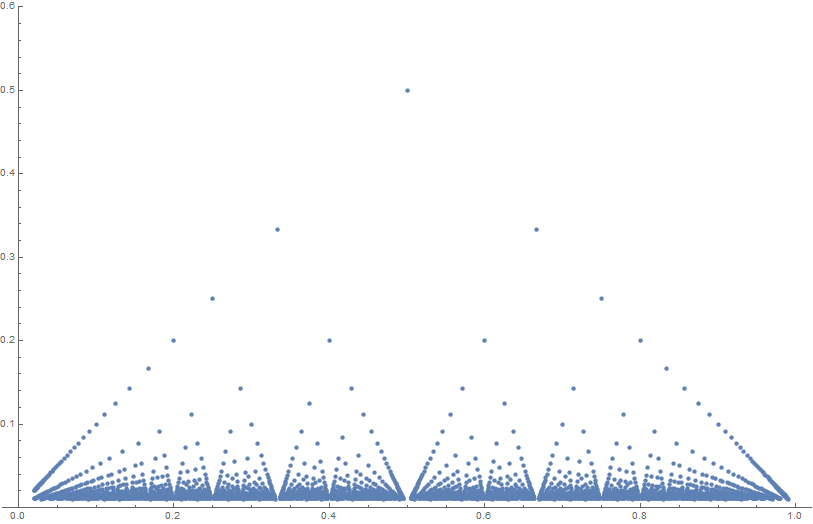
Thomae's function (sometimes called the popcorn function, raindrop function, Stars over Babylon) is given by the formula $$f(x) =\begin{cases} 1 & \text{if } x= 0 \\ \tfrac1{q} & \text{if } x = \tfrac{p}{q}\\ 0 & \text{if } x \in \mathbb{R}-\mathbb{Q}. \end{cases}$$
Plot of the Thomae function.
Properties
Thomae function is continuous at irrationals
Thomae function is discontinuous at rationals
Theorem: The Thomae function has a (strict) local maximum at each rational number.
Proof: █
Theorem: The Thomae function $f(x)$ is Riemann integrable and $$\displaystyle\int_0^1 f(x) \mathrm{d}x = 0.$$
Proof: █
Videos
Thomae Function by Bret Benesh (11 January 2012)
Thomae Function by Douglas Harder (19 April 2012)
See also
Modifications of Thomae's Function and Differentiability
