Difference between revisions of "Dirichlet beta"
From specialfunctionswiki
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
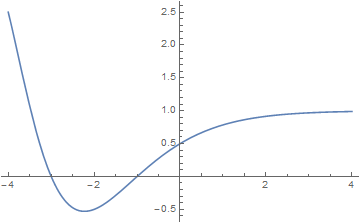
The Dirichlet $\beta$ function is defined by | The Dirichlet $\beta$ function is defined by | ||
| − | $$\beta(x) = \displaystyle\sum_{k=0}^{\infty} (-1)^k (2k+1)^{-x} | + | $$\beta(x) = \displaystyle\sum_{k=0}^{\infty} (-1)^k (2k+1)^{-x}.$$ |
| − | |||
| Line 14: | Line 13: | ||
=Properties= | =Properties= | ||
[[Catalan's constant using Dirichlet beta]]<br /> | [[Catalan's constant using Dirichlet beta]]<br /> | ||
| + | [[Dirichlet beta in terms of Lerch transcendent]]<br /> | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 00:51, 11 December 2016
The Dirichlet $\beta$ function is defined by $$\beta(x) = \displaystyle\sum_{k=0}^{\infty} (-1)^k (2k+1)^{-x}.$$
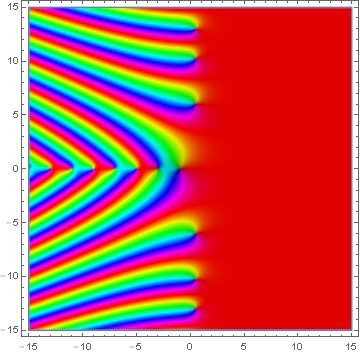
Domain coloring of analytic continuation of $\beta$.
Properties
Catalan's constant using Dirichlet beta
Dirichlet beta in terms of Lerch transcendent