Difference between revisions of "Floor"
From specialfunctionswiki
(Created page with "The floor function $\lfloor \cdot \rfloor \colon \mathbb{R} \rightarrow \mathbb{Z}$ is defined by $$\lfloor x \rfloor = \max \left\{y \in \mathbb{Z} \colon y \leq x \right\},$...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The floor function $\ | + | The floor function $\mathrm{floor} \colon \mathbb{R} \rightarrow \mathbb{Z}$ (sometimes written as $\lfloor x \rfloor$) is defined by |
| − | $$\lfloor x \rfloor = \max \left\{y \in \mathbb{Z} \colon y \leq x \right\},$$ | + | $$\mathrm{floor}(x) \equiv \lfloor x \rfloor = \max \left\{y \in \mathbb{Z} \colon y \leq x \right\},$$ |
| − | i.e., it is the largest [[integer]] less than or equal to $x$. | + | i.e., it is the largest [[integer]] less than or equal to $x$. |
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
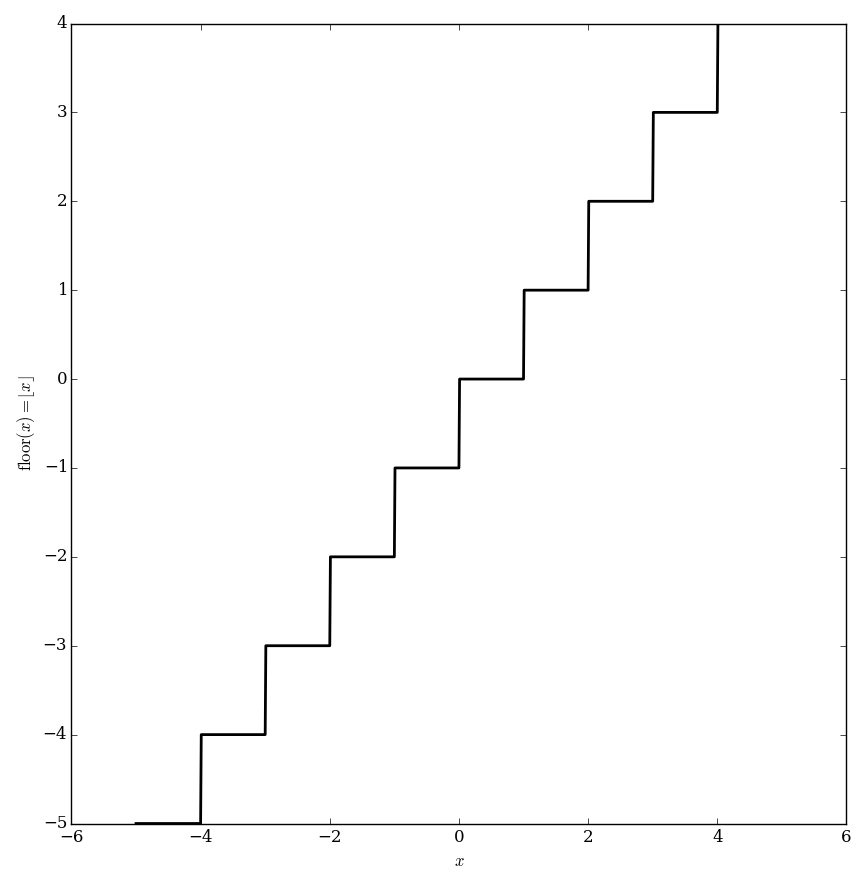
| + | File:Floorplot.png|Graph of $\mathrm{floor}$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =See Also= | ||
| + | [[Ceiling]]<br /> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 00:41, 23 December 2016
The floor function $\mathrm{floor} \colon \mathbb{R} \rightarrow \mathbb{Z}$ (sometimes written as $\lfloor x \rfloor$) is defined by $$\mathrm{floor}(x) \equiv \lfloor x \rfloor = \max \left\{y \in \mathbb{Z} \colon y \leq x \right\},$$ i.e., it is the largest integer less than or equal to $x$.