Difference between revisions of "Prime zeta P"
From specialfunctionswiki
(→References) |
(→Videos) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
=Properties= | =Properties= | ||
| + | [[Derivative of prime zeta]]<br /> | ||
[[Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta]]<br /> | [[Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta]]<br /> | ||
| + | |||
| + | =Videos= | ||
| + | [https://www.youtube.com/watch?v=3eN9tQX3JJ4 Zeta Function - Part 5 - Prime Zeta Function] (15 March 2012)<br /> | ||
| + | |||
| + | =External links= | ||
| + | [http://math.stackexchange.com/questions/49383/how-does-sum-px-p-s-grow-asymptotically-for-textres-1/ How does ∑p<xp−s grow asymptotically for Re(s)<1?] <br /> | ||
| + | [http://math.stackexchange.com/questions/504445/zeta-question-prime-zeta-basic-calculus Zeta question - prime zeta. Basic calculus]<br /> | ||
| + | [http://math.stackexchange.com/questions/799590/prime-zeta-function Prime Zeta Function]<br /> | ||
| + | [http://math.stackexchange.com/questions/32974/prime-zeta-definition-multiplication-by-zero Prime zeta definition, multiplication by zero]<br /> | ||
| + | [http://math.stackexchange.com/questions/1029976/closed-form-of-prime-zeta-values Closed-form of prime zeta values]<br /> | ||
| + | [http://math.stackexchange.com/questions/1537551/zeros-of-the-prime-zeta-function Zeros of the prime zeta function]<br /> | ||
| + | [http://math.stackexchange.com/questions/246770/infinite-sum-of-powers-of-the-prime-zeta-function Infinite sum of powers of the prime zeta function]<br /> | ||
| + | [http://math.stackexchange.com/questions/1615626/convergence-of-prime-zeta-function-for-mathfrak-rs-1 Convergence of prime zeta function for R(s)=1?]<br /> | ||
=References= | =References= | ||
* {{PaperReference|The Sums of the Series of the Reciprocals of the Prime Numbers and of Their Powers|1881|Charles Watkins Merrifield}} | * {{PaperReference|The Sums of the Series of the Reciprocals of the Prime Numbers and of Their Powers|1881|Charles Watkins Merrifield}} | ||
* {{PaperReference|On the Sums of the Inverse Powers of the Prime Numbers|1891|James Whitbread Lee Glaisher}} | * {{PaperReference|On the Sums of the Inverse Powers of the Prime Numbers|1891|James Whitbread Lee Glaisher}} | ||
| − | + | * {{PaperReference|On the prime zeta function|1968|Carl-Erik Fröberg}} | |
| − | |||
| − | |||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 23:29, 17 March 2017
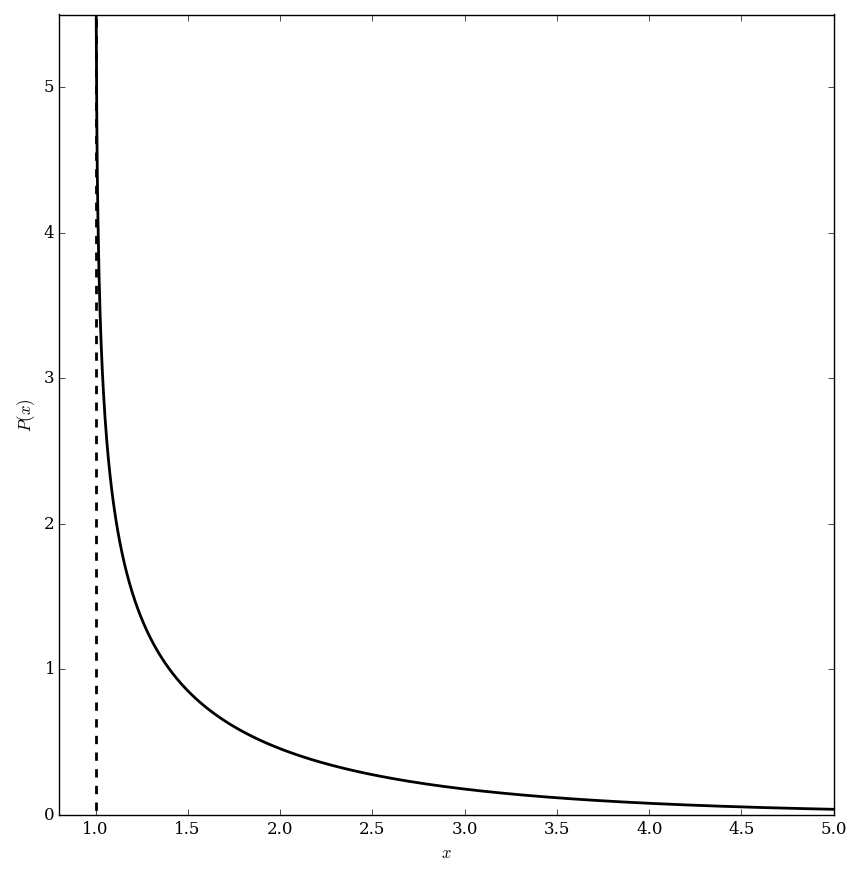
The prime zeta function is defined by $$P(z) = \displaystyle\sum_{p \mathrm{\hspace{2pt} prime}} \dfrac{1}{p^z},$$ where $\mathrm{Re}(z)>1$. It can be extended outside of this domain via analytic continuation.
Properties
Derivative of prime zeta
Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta
Videos
Zeta Function - Part 5 - Prime Zeta Function (15 March 2012)
External links
How does ∑p<xp−s grow asymptotically for Re(s)<1?
Zeta question - prime zeta. Basic calculus
Prime Zeta Function
Prime zeta definition, multiplication by zero
Closed-form of prime zeta values
Zeros of the prime zeta function
Infinite sum of powers of the prime zeta function
Convergence of prime zeta function for R(s)=1?