Difference between revisions of "Polylogarithm"
From specialfunctionswiki
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
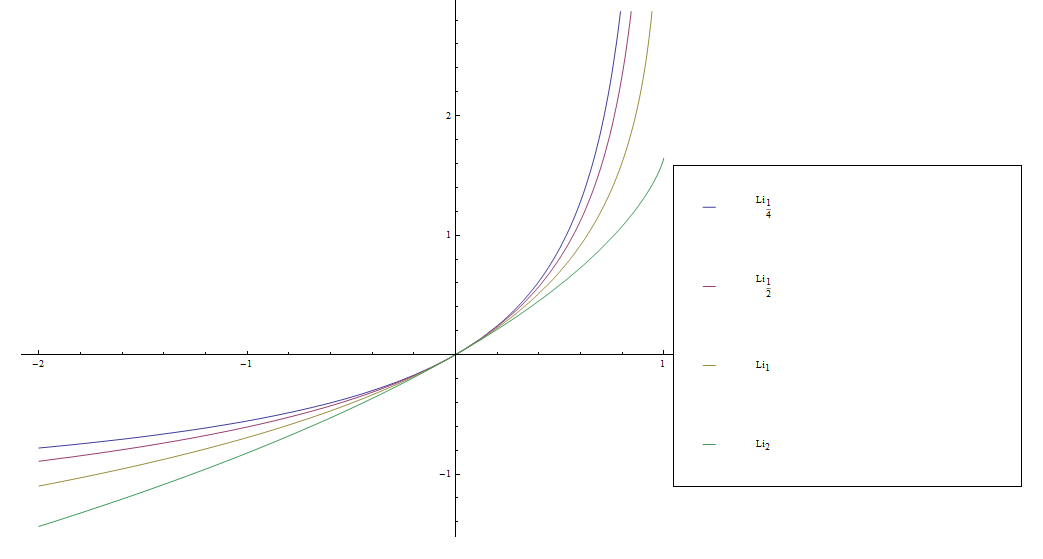
The polylogarithm $\mathrm{Li}_s$ is defined by the formula for $|z|<1$ by | The polylogarithm $\mathrm{Li}_s$ is defined by the formula for $|z|<1$ by | ||
| − | $$\mathrm{Li}_s(z) = \sum_{k=1}^{\infty} \dfrac{z^k}{k^ | + | $$\mathrm{Li}_s(z) = \sum_{k=1}^{\infty} \dfrac{z^k}{k^z} = z + \dfrac{z^2}{2^z} + \dfrac{z^3}{3^z} + \ldots$$ |
A special case of the polylogarithm with $s=2$ is called a [[dilogarithm]]. | A special case of the polylogarithm with $s=2$ is called a [[dilogarithm]]. | ||
Revision as of 17:03, 19 April 2017
The polylogarithm $\mathrm{Li}_s$ is defined by the formula for $|z|<1$ by $$\mathrm{Li}_s(z) = \sum_{k=1}^{\infty} \dfrac{z^k}{k^z} = z + \dfrac{z^2}{2^z} + \dfrac{z^3}{3^z} + \ldots$$ A special case of the polylogarithm with $s=2$ is called a dilogarithm.
Various polylogarithms plotted on $[-2,1]$.
Properties
Lerch transcendent polylogarithm
Legendre chi in terms of polylogarithm
