Difference between revisions of "Bessel Y"

From specialfunctionswiki
Jump to: navigation, search
 
(11 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
Bessel functions of the second kind $Y_{\nu}$ are defined via the formula
+
Bessel functions of the second kind, $Y_{\nu}$, are defined via the formula
 
$$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$
 
$$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$
 
Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$.
 
Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$.
Line 5: Line 5:
 
<div align="center">
 
<div align="center">
 
<gallery>
 
<gallery>
−
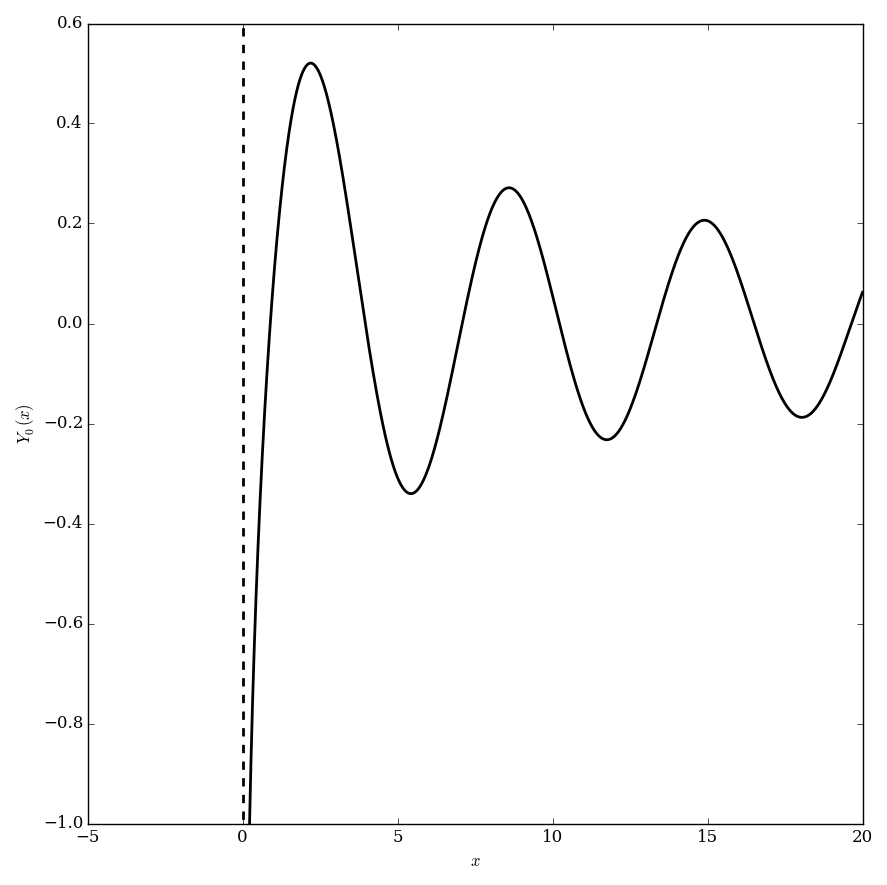
File:Bessel y plot.png|Graph of $Y_0,Y_1,\ldots,Y_5$ on $[0,20]$.
+
File:Bessely,n=0plot.png|Graph of $Y_0$.
−
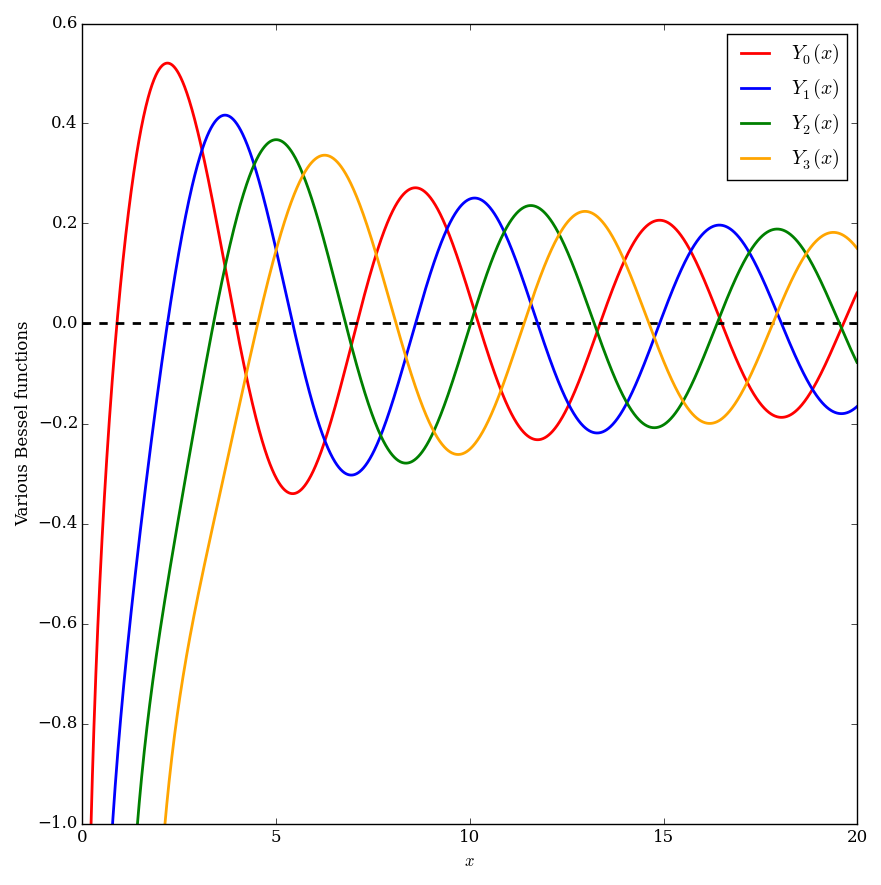
File:Complex bessel y sub 0.png|[[Domain coloring]] of $Y_0(z)$.
+
File:Multiplebesselyplot.png|Graph of $Y_0,Y_1,Y_2$, and $Y_3$.
−
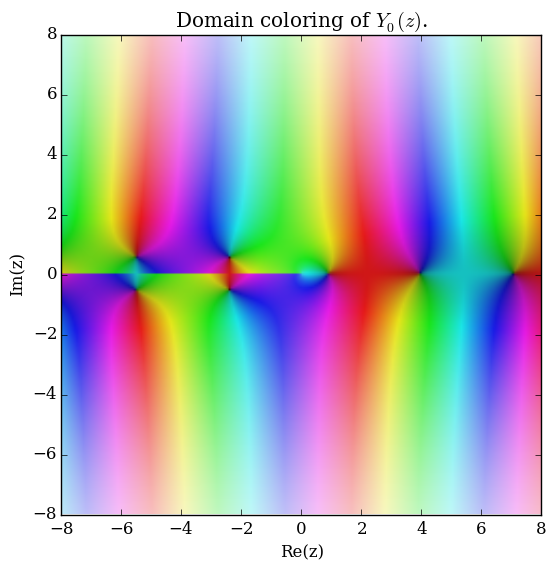
File:Domcolbesselysub1.png|[[Domain coloring]] of $Y_1(z)$.
+
File:Complexbessely,n=0.png|[[Domain coloring]] of $Y_0$.
 +
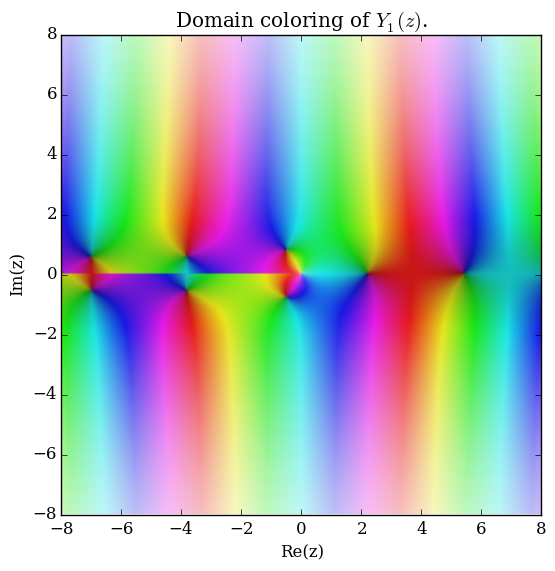
File:Complexbessely,n=1.png|[[Domain coloring]] of $Y_1$.
 
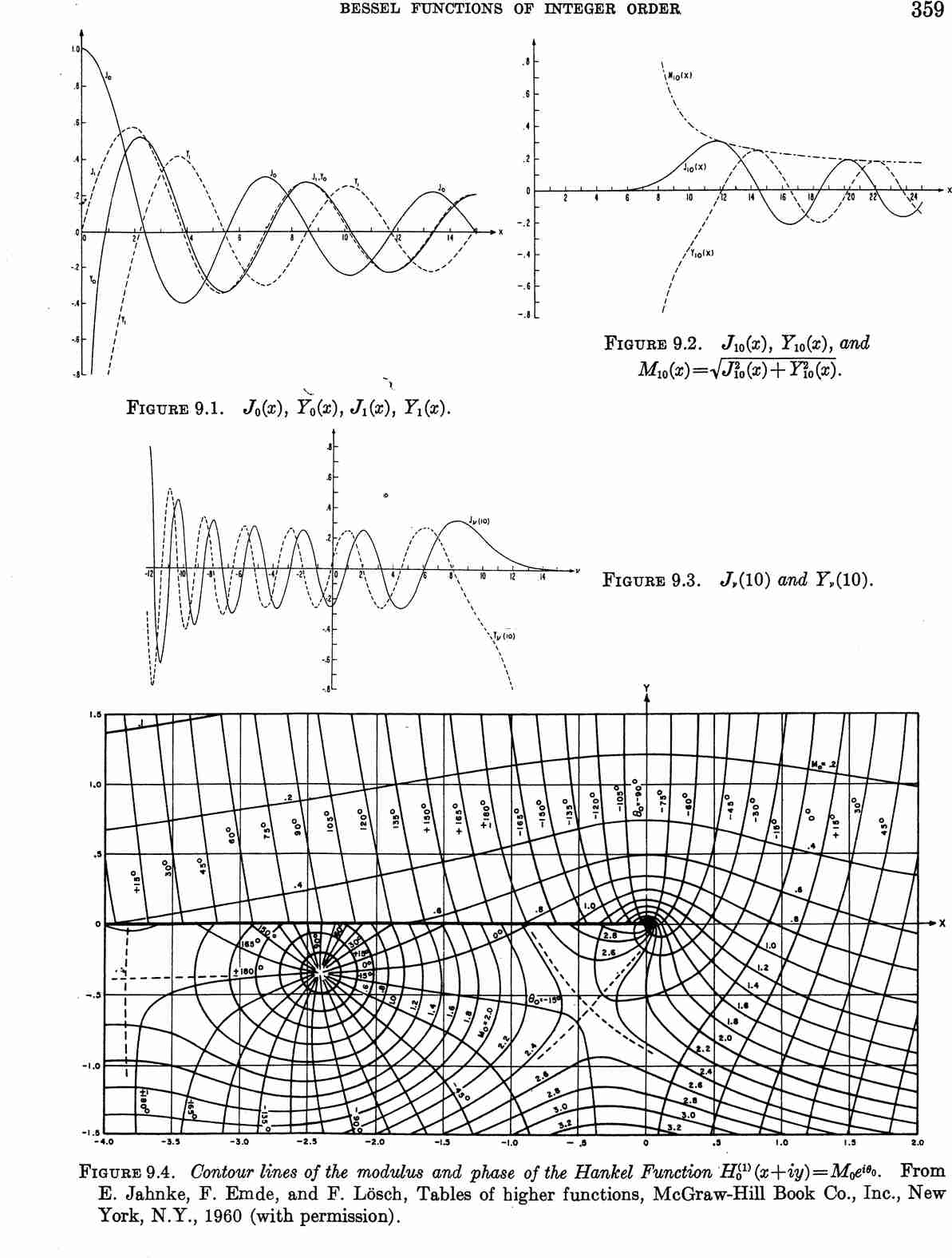
File:Page 359Abramowitz-Stegun(Bessel functions).jpg|Bessel functions from [http://dualaud.net/specialfunctionswiki/abramowitz_and_stegun-1.03/ Abramowitz&Stegun]
 
File:Page 359Abramowitz-Stegun(Bessel functions).jpg|Bessel functions from [http://dualaud.net/specialfunctionswiki/abramowitz_and_stegun-1.03/ Abramowitz&Stegun]
 
</gallery>
 
</gallery>
Line 15: Line 16:
  
 
=Properties=
 
=Properties=
−
<div class="toccolours mw-collapsible mw-collapsed">
+
[[Derivative of Bessel Y with respect to its order]]
−
<strong>Theorem:</strong> The following formula holds for $n \in \mathbb{Z}$:
 
−
$$Y_{-n}(z)=(-1)^nY_n(z).$$
 
−
<div class="mw-collapsible-content">
 
−
<strong>Proof:</strong> █
 
−
</div>
 
−
</div>
 
−
 
 
−
{{:Bessel J sub nu and Y sub nu solve Bessel's differential equation}}
 
−
 
 
−
{{:Bessel J sub nu and Y sub nu solve Bessel's differential equation (constant multiple in argument)}}
 
−
 
 
−
<div class="toccolours mw-collapsible mw-collapsed">
 
−
<strong>Theorem:</strong> The following formula holds for $n\in\mathbb{Z}$:
 
−
$${\small Y_n(z)=\dfrac{2}{\pi} \left[ \log \left( \dfrac{z}{2} \right)+\gamma-\dfrac{1}{2}\displaystyle\sum_{k=1}^n \dfrac{1}{k} \right]J_n(x) - \dfrac{1}{\pi} \displaystyle\sum_{k=0}^{\infty} (-1)^k \dfrac{1}{k!(n+k)!} \left(\dfrac{z}{2}\right)^{n+2k}\displaystyle\sum_{j=1}^k \left( \dfrac{1}{j} + \dfrac{1}{j+n} \right) - \dfrac{1}{\pi}\displaystyle\sum_{k=0}^{n-1} \dfrac{(n-k-1)!}{k!} \left( \dfrac{z}{2} \right)^{-n+2k},}$$
 
−
where $Y_n$ denotes the [[Bessel Y sub nu|Bessel function of the second kind]], $\log$ denotes the [[logarithm]], $\gamma$ denotes the [[Euler-Mascheroni constant]], and $J_n$ denotes the [[Bessel J sub nu|Bessel function of the first kind]].
 
−
<div class="mw-collapsible-content">
 
−
<strong>Proof:</strong> █
 
−
</div>
 
−
</div>
 
  
 
=References=
 
=References=
 +
* {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Hankel H (1)}}: 9.1.2
 
[http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0021%7CLOG_0023 Bessel's functions of the second order - C.V. Coates]<br />
 
[http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0021%7CLOG_0023 Bessel's functions of the second order - C.V. Coates]<br />
−
<center>{{:Bessel functions footer}}</center>
+
 
 +
{{:Bessel functions footer}}
  
 
[[Category:SpecialFunction]]
 
[[Category:SpecialFunction]]

Latest revision as of 15:39, 10 July 2017

Bessel functions of the second kind, $Y_{\nu}$, are defined via the formula $$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$ Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$.


Properties

Derivative of Bessel Y with respect to its order

References

Bessel's functions of the second order - C.V. Coates

Bessel functions

Anger function

Bessel-Clifford

Bessel $J_{\nu}$

Bessel $Y_{\nu}$

Bessel $I_{\nu}$

Modified Bessel $K_{\nu}$

Spherical Bessel $j_{\nu}$

Spherical Bessel $y_{\nu}$
Retrieved from "http://specialfunctionswiki.org/index.php?title=Bessel_Y&oldid=8678"