Difference between revisions of "Debye function"
From specialfunctionswiki
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
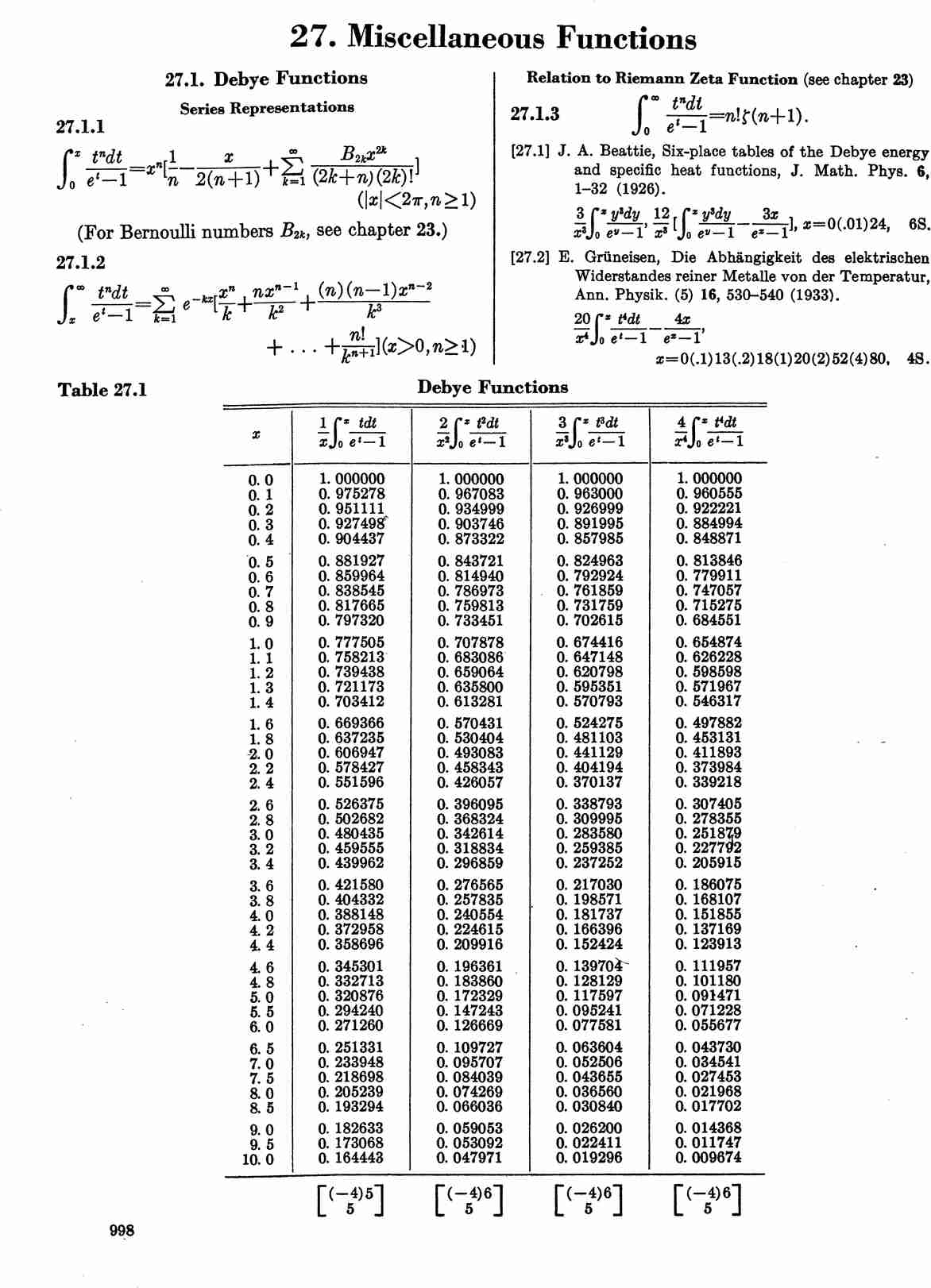
| − | The Debye functions are defined by | + | The Debye functions, $D_n$, are defined by |
| − | $$D_n(x)=\dfrac{n}{x^n} \displaystyle\int_0^x \dfrac{t^n}{e^t-1} | + | $$D_n(x)=\dfrac{n}{x^n} \displaystyle\int_0^x \dfrac{t^n}{e^t-1} \mathrm{d}t.$$ |
<div align="center"> | <div align="center"> | ||
| Line 7: | Line 7: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | =Properties= | ||
| + | |||
| + | =References= | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 15:56, 10 July 2017
The Debye functions, $D_n$, are defined by $$D_n(x)=\dfrac{n}{x^n} \displaystyle\int_0^x \dfrac{t^n}{e^t-1} \mathrm{d}t.$$
Abramowitz&Stegun, pg.998.
