Difference between revisions of "Dawson D+"
From specialfunctionswiki
(Created page with "The Dawson function $D+$ is defined by $$D_+(x)=e^{-x^2}\displaystyle\int_0^x e^{t^2} dt,$$ where $e^{-x^2}$ denotes the exponential. =Properties= =References= Catego...") |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The Dawson function $D+$ is defined by | + | The Dawson function $D+$ (sometimes called the Dawson $F$ function) is defined by |
| − | $$D_+(x)=e^{-x^2}\displaystyle\int_0^x e^{t^2} | + | $$D_+(x)=e^{-x^2}\displaystyle\int_0^x e^{t^2} \mathrm{d}t,$$ |
where $e^{-x^2}$ denotes the [[exponential]]. | where $e^{-x^2}$ denotes the [[exponential]]. | ||
| + | |||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
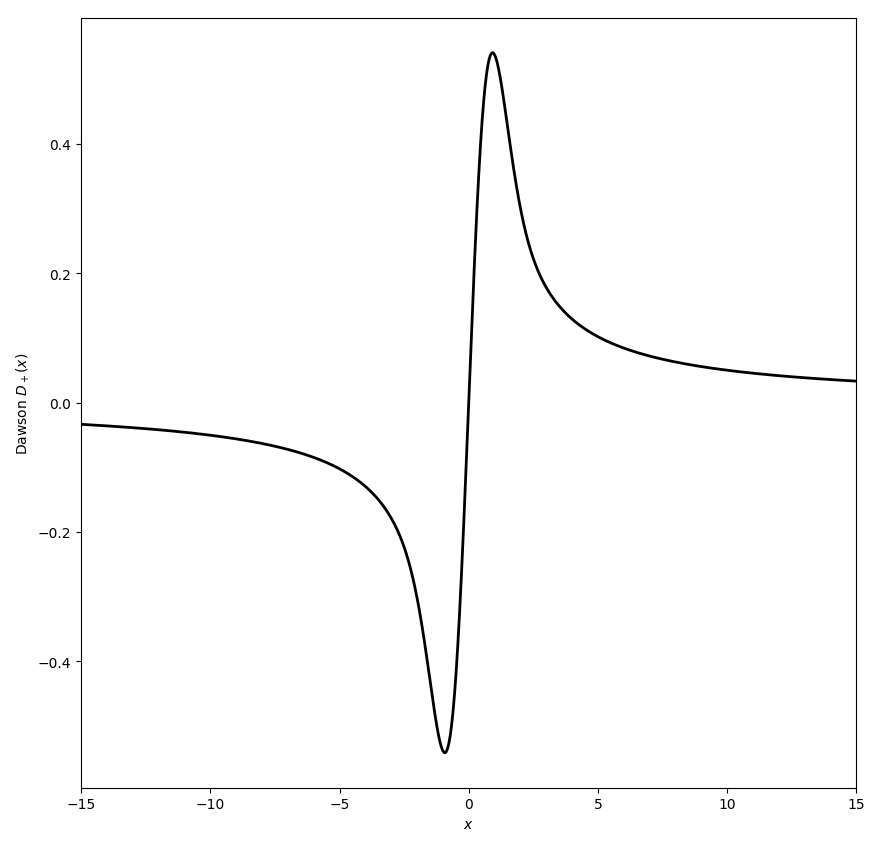
| + | File:Dawsondplusplot.png|Plot of $D_+$ on $[-15,15]$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
| + | |||
| + | =See also= | ||
| + | [[Dawson D-]]<br /> | ||
| + | [[Error function]]<br /> | ||
| + | [[Faddeeva function]]<br /> | ||
=References= | =References= | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 00:21, 29 October 2017
The Dawson function $D+$ (sometimes called the Dawson $F$ function) is defined by $$D_+(x)=e^{-x^2}\displaystyle\int_0^x e^{t^2} \mathrm{d}t,$$ where $e^{-x^2}$ denotes the exponential.
Properties
See also
Dawson D-
Error function
Faddeeva function