Difference between revisions of "Elliptic K"
From specialfunctionswiki
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
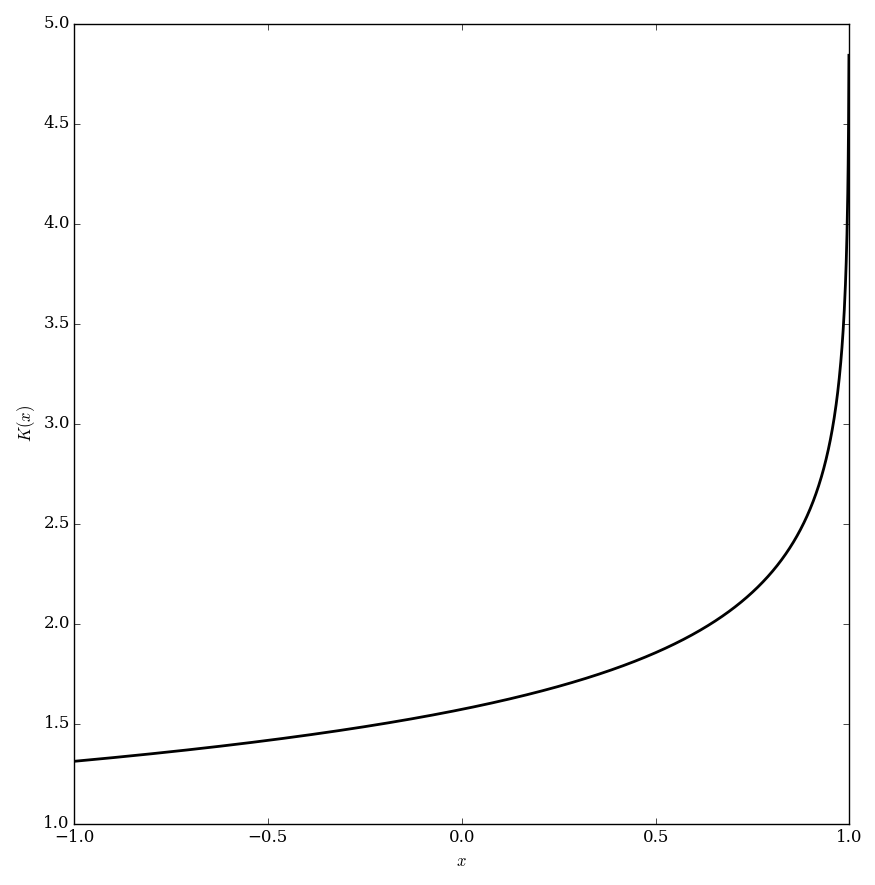
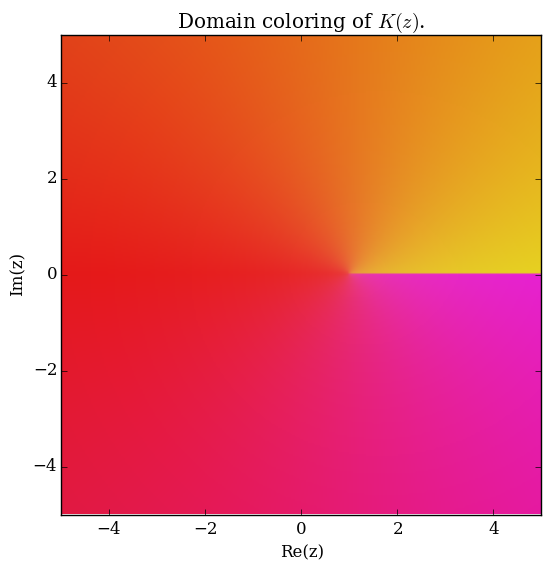
| − | The | + | The elliptic $K$ function (also known as the complete elliptic integral of the first kind) is defined by |
| − | $$ | + | $$K(m)=\displaystyle\int_0^{\frac{\pi}{2}} \dfrac{1}{\sqrt{1-m\sin^2 \theta}} \mathrm{d}\theta.$$ |
<div align="center"> | <div align="center"> | ||
| Line 8: | Line 8: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[K(m)=(pi/2)2F1(1/2,1/2;1;m)]]<br /> | ||
=See Also= | =See Also= | ||
| Line 14: | Line 17: | ||
=References= | =References= | ||
| − | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=findme}}: $17.3.1$ | |
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 04:48, 21 December 2017
The elliptic $K$ function (also known as the complete elliptic integral of the first kind) is defined by $$K(m)=\displaystyle\int_0^{\frac{\pi}{2}} \dfrac{1}{\sqrt{1-m\sin^2 \theta}} \mathrm{d}\theta.$$
Graph of $K$.
Domain coloring of $K$.
Properties
See Also
Elliptic E
Incomplete Elliptic K
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $17.3.1$
