Difference between revisions of "Elliptic E"
From specialfunctionswiki
(Created page with "If $m=k^2$ we define the complete elliptic integral of the second kind, $E$, to be $$E(k)=E(m)=\displaystyle\int_0^{\frac{\pi}{2}} \sqrt{1-k^2\sin^2 \theta} d\theta.$$ The inc...") |
|||
| (12 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
If $m=k^2$ we define the complete elliptic integral of the second kind, $E$, to be | If $m=k^2$ we define the complete elliptic integral of the second kind, $E$, to be | ||
| − | $$E(k)=E(m)=\displaystyle\int_0^{\frac{\pi}{2}} \sqrt{1-k^2\sin^2 \theta} d\theta.$$ | + | $$E(k)=E(m)=\displaystyle\int_0^{\frac{\pi}{2}} \sqrt{1-k^2\sin^2 \theta} \mathrm{d}\theta.$$ |
| − | + | ||
| − | $$E( | + | <div align="center"> |
| + | <gallery> | ||
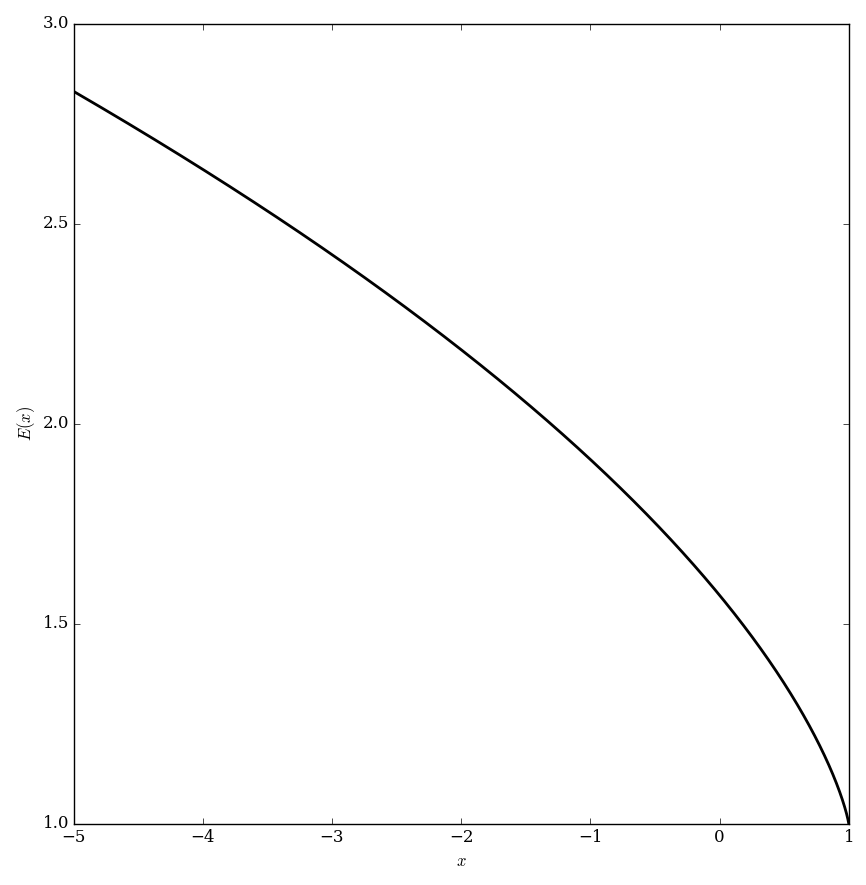
| + | File:Ellipticeplot.png|Graph of $E$. | ||
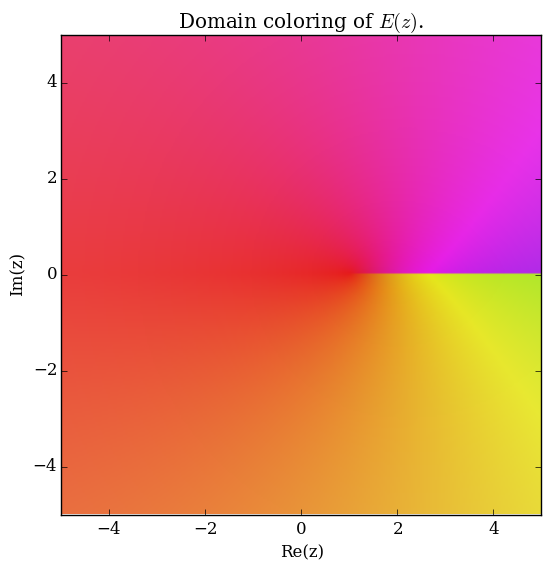
| + | File:Complexellipticeplot.png|[[Domain coloring]] of $E$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[E(m)=(pi/2)2F1(-1/2,1/2;1;m)]]<br /> | ||
| + | |||
| + | =See Also= | ||
| + | [[Elliptic K]] <br /> | ||
| + | [[Incomplete Elliptic E]] | ||
| + | |||
| + | =References= | ||
| + | [http://web.mst.edu/~lmhall/SPFNS/spfns.pdf "Special Functions" by Leon Hall] | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 04:54, 21 December 2017
If $m=k^2$ we define the complete elliptic integral of the second kind, $E$, to be $$E(k)=E(m)=\displaystyle\int_0^{\frac{\pi}{2}} \sqrt{1-k^2\sin^2 \theta} \mathrm{d}\theta.$$
Domain coloring of $E$.
Properties
See Also
Elliptic K
Incomplete Elliptic E