Difference between revisions of "Dedekind eta"
From specialfunctionswiki
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Let $q=e^{2\pi i | + | Let $q=e^{2\pi i z}$, where $z$ is in the upper half plane. We define the Dedekind eta function by the formula |
| − | $$\eta( | + | $$\eta(z) = e^{\frac{\pi i z}{12}} \displaystyle\prod_{n=1}^{\infty} (1-q^n).$$ |
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
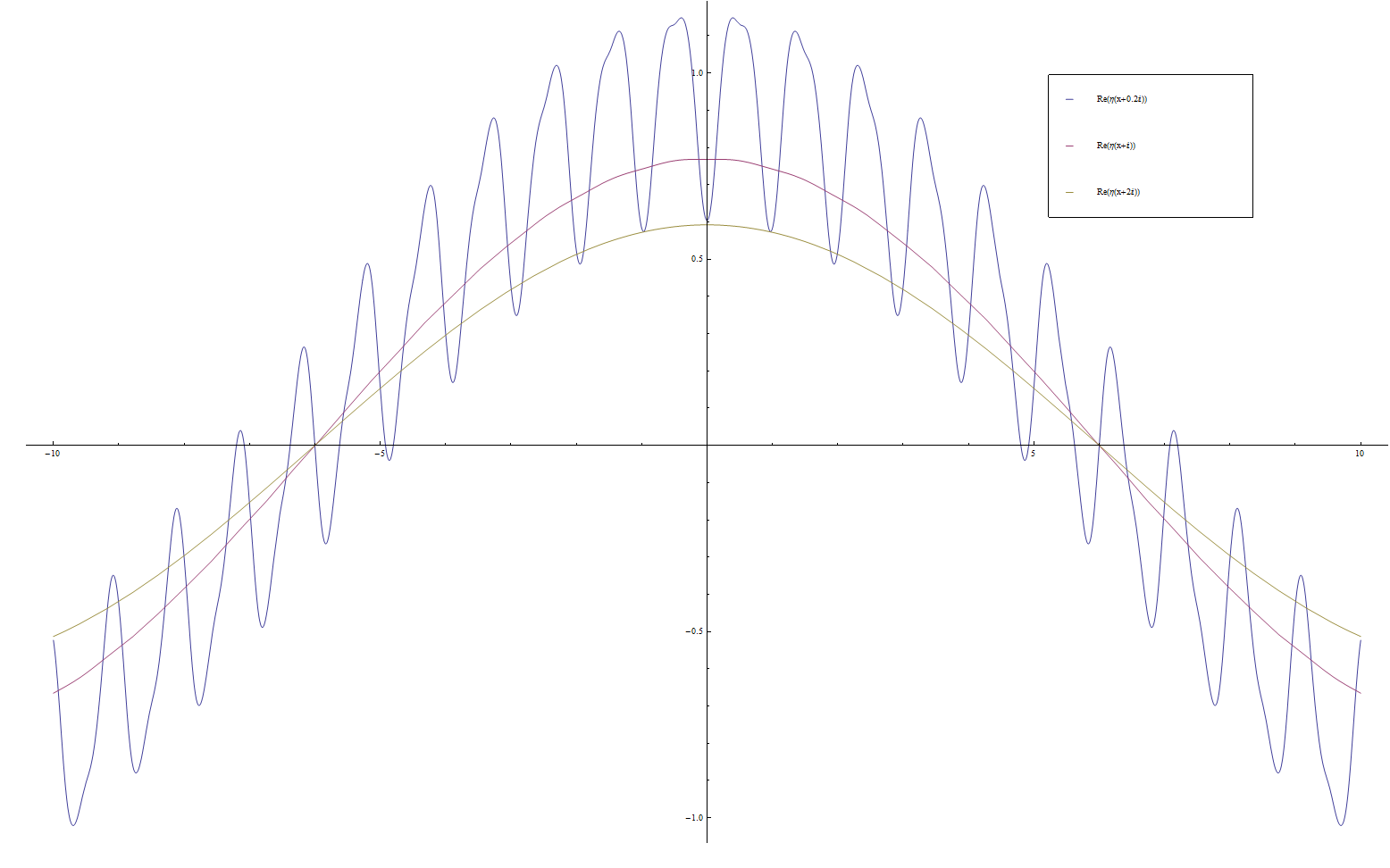
| + | File:DedekindetaRe.png|Real part of $\eta$. | ||
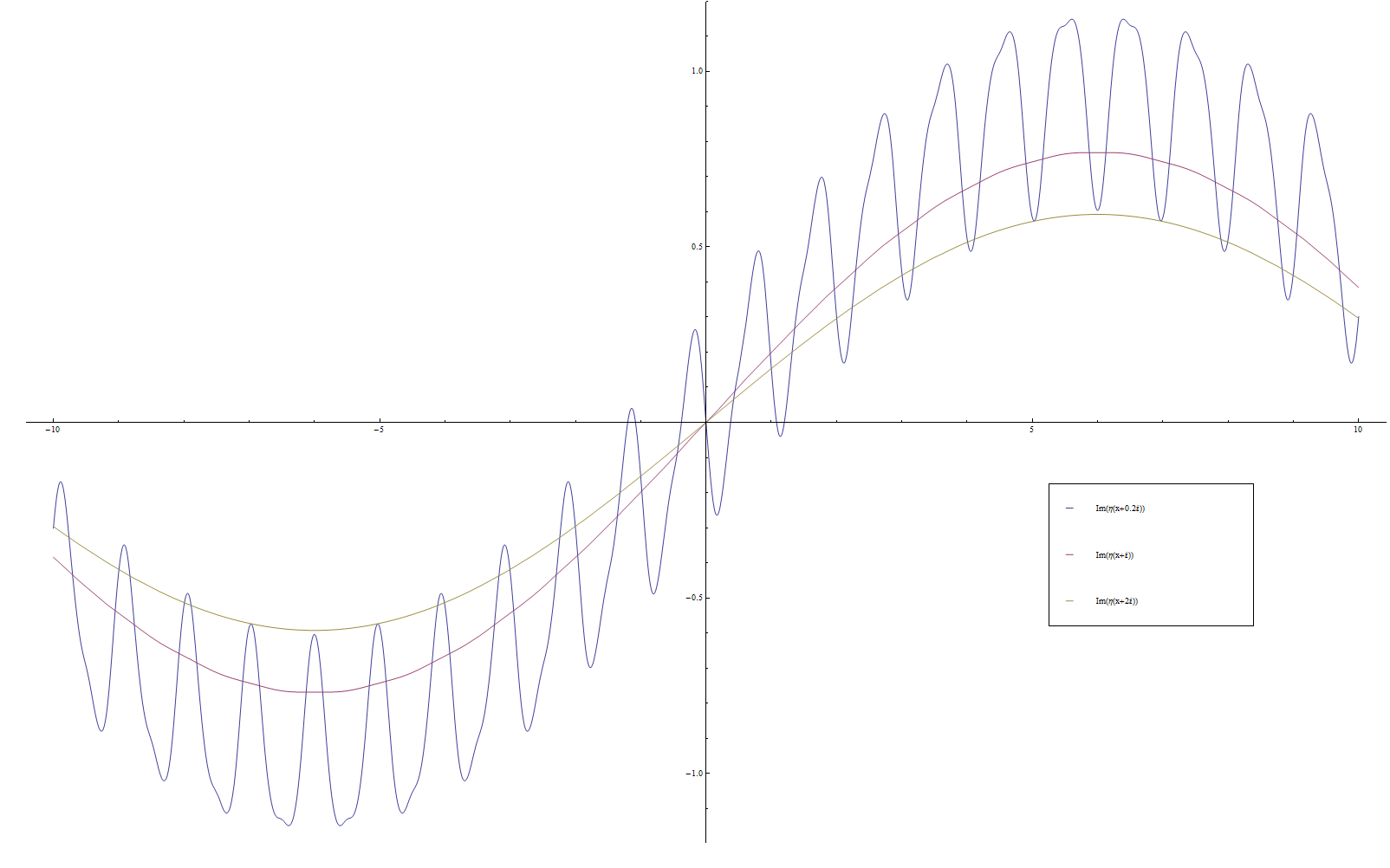
| + | File:DedekindetaIm.png|Imaginary part of $\eta$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[eta(z+1)=e^(i pi/12)eta(z)]]<br /> | ||
| + | [[eta(-1/z)=sqrt(-iz)eta(z)]]<br /> | ||
| + | |||
| + | =References= | ||
| + | [http://eta.math.georgetown.edu/ A collection of over 6200 identities for the Dedekind Eta Function] | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 05:20, 12 February 2018
Let $q=e^{2\pi i z}$, where $z$ is in the upper half plane. We define the Dedekind eta function by the formula $$\eta(z) = e^{\frac{\pi i z}{12}} \displaystyle\prod_{n=1}^{\infty} (1-q^n).$$
Real part of $\eta$.
Imaginary part of $\eta$.
Properties
eta(z+1)=e^(i pi/12)eta(z)
eta(-1/z)=sqrt(-iz)eta(z)
References
A collection of over 6200 identities for the Dedekind Eta Function
