Difference between revisions of "Digamma"
From specialfunctionswiki
| (11 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The digamma function $\psi$ is defined by | + | The digamma function $\psi \colon \mathbb{C} \setminus \{0,-1,-2,\ldots\} \rightarrow \mathbb{C}$ is defined by |
| − | $$\psi(z) = \dfrac{d}{ | + | $$\psi(z) = \dfrac{\mathrm{d}}{\mathrm{d}z} \log \Gamma(z) = \dfrac{\Gamma'(z)}{\Gamma(z)}.$$ |
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
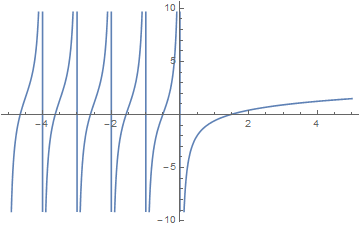
| − | File:Plot digamma.png|Graph of $\psi | + | File:Plot digamma.png|Graph of $\psi$. |
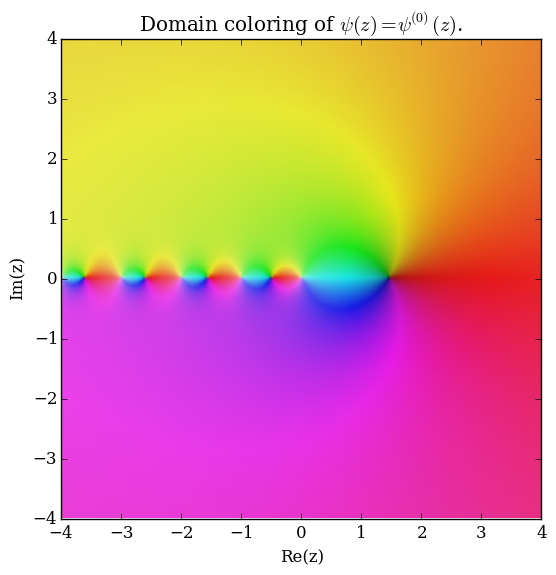
| − | File: | + | File:Complexdigammaplot.png|[[Domain coloring]] of $\psi(z)$. |
</gallery> | </gallery> | ||
</div> | </div> | ||
| − | |||
| − | |||
=Properties= | =Properties= | ||
| − | < | + | [[Partial derivative of beta function]]<br /> |
| − | + | [[Digamma at 1]]<br /> | |
| − | + | [[Digamma functional equation]]<br /> | |
| − | + | [[Digamma at n+1]]<br /> | |
| − | |||
| − | </ | ||
| − | </ | ||
| − | + | =See Also= | |
| − | + | [[Gamma]] <br /> | |
| − | + | [[Polygamma]]<br /> | |
| − | + | [[Trigamma]] <br /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | </ | ||
| − | + | =References= | |
| − | + | * {{BookReference|Higher Transcendental Functions Volume I|1953|Arthur Erdélyi|author2=Wilhelm Magnus|author3=Fritz Oberhettinger|author4=Francesco G. Tricomi|prev=findme|next=findme}}: $\S 1.7 (1)$ | |
| − | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Beta is symmetric|next=Digamma at 1}}: $6.3.1$ | |
| − | |||
| − | |||
| − | |||
| − | + | [[Category:SpecialFunction]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[ | ||
| − | |||
| − | |||
Latest revision as of 23:21, 3 March 2018
The digamma function $\psi \colon \mathbb{C} \setminus \{0,-1,-2,\ldots\} \rightarrow \mathbb{C}$ is defined by $$\psi(z) = \dfrac{\mathrm{d}}{\mathrm{d}z} \log \Gamma(z) = \dfrac{\Gamma'(z)}{\Gamma(z)}.$$
Domain coloring of $\psi(z)$.
Properties
Partial derivative of beta function
Digamma at 1
Digamma functional equation
Digamma at n+1
See Also
References
- 1953: Arthur Erdélyi, Wilhelm Magnus, Fritz Oberhettinger and Francesco G. Tricomi: Higher Transcendental Functions Volume I ... (previous) ... (next): $\S 1.7 (1)$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $6.3.1$